
【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为![]() AC·BD.
AC·BD.
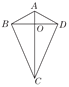
【答案】①③⑤
【解析】
根据题意AB=AD,BC=DC,AC与BD相交于点O可以证明△ABC≌△ADC、△ABO≌△ADO,可得AC、BD互相垂直,AC平分∠BAD、∠BCD.
∵在△ABC与△ADC中, ,∴△ABC≌△ADC(SSS),∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
,∴△ABC≌△ADC(SSS),∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
∵AC平分∠BAD、∠BCD,△ABD与△BCD均为等腰三角形,∴AC、BD互相垂直,但不平分.故①正确,②错误;
由题中条件无法证明∠ABC=∠ADC=90°,故④错误;
∵AC、BD互相垂直,∴筝形ABCD的面积为:![]() ACBO
ACBO![]() ACOD
ACOD![]() ACBD.
ACBD.
故⑤正确;
综上所述:正确的说法是①③⑤.
故答案为:①③⑤.


科目:初中数学 来源: 题型:
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为 ![]() (元)、
(元)、 ![]() (元),猜想
(元),猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t;5辆大货车与6辆小货车一次可以运货35t
(1)每辆大货车和每辆小货车一次各可以运货多少?
(2)现在租用这两种火车共10辆,要求一次运输货物不低于30t,则大货车至少租几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
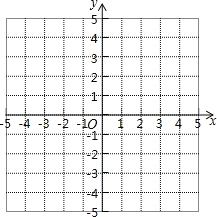
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
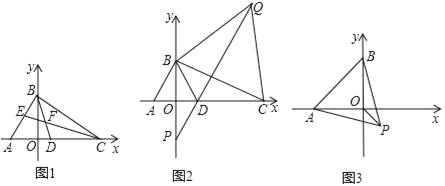
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
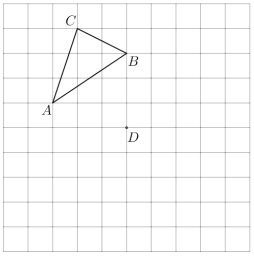
【题目】在图中网格上按要求画出图形,并回答问题:
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() 是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
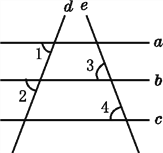
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于点O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
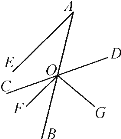
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com