
【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t;5辆大货车与6辆小货车一次可以运货35t
(1)每辆大货车和每辆小货车一次各可以运货多少?
(2)现在租用这两种火车共10辆,要求一次运输货物不低于30t,则大货车至少租几辆?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
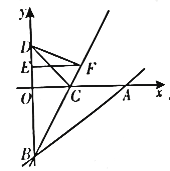
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
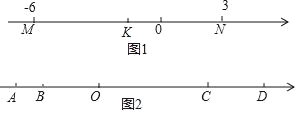
如图1,在数轴上点M表示的数是﹣6,点N表示的数是3,求线段MN的中点K所示的数.
对于求中点表示数的问题,只要用点N所表示的数3,加上点M所表示的数﹣6,得到的结果再除以2,就可以得到中点K所表示的数;即K点表示的数为![]() =﹣1.5
=﹣1.5
利用材料中知识解决下面问题:
如图2,已知数轴上有A、B、C、D四点,A点表示数为﹣6,B点表示的数是﹣4,线段AD=18,BC=3CD.
(1)点D所表示的数是 ;
(2)若点B以每秒4个单位的速度向右运动,点D以每秒1个单位的速度向左运动,同时运动t秒后,当点C为线段BD的中点时,求t的值;
(3)若(2)中点B、点D的运动速度运动方向不变,点A以每秒10个单位的速度向右运动,点C以每秒3个单位的速度向左运动,点P是线段AC的中点,点Q是线段BD的中点,A、B、C、D四点同时运动,运动时间为t,求线段PQ的长(用含t的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题
(1)2015年比2011年增加 人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请按要求完成下面三道小题.
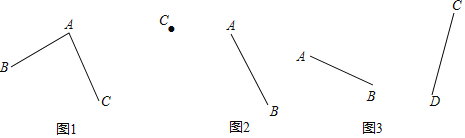
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图2,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且A与C是对称点,明对称轴b,并简述画图过程.
(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线,在△ABC中,∠B=30°,AD和 DE是△ABC的三分线,点D在 BC 边上,点E在 AC边上,且AD=BD,DE=CE,请写出∠C所有可能的度数________.
查看答案和解析>>
科目:初中数学 来源: 题型:
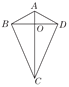
【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为![]() AC·BD.
AC·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依法纳税是每个公民应尽的义务.新税法规定:居民个人的综合所得,以每一纳税月收入减去费用5000元以及专项扣除、专项附加扣除和依法确定的其它扣除后的余额,为个人应纳税所得额.已知李先生某月的个人应纳税所得额比张先生的多1500元,个人所得税税率相同情况下,李先生的个人所得税税额为76.5元,而张先生的个人所得税税额为31.5元.求李先生和张先生应纳税所得额分别为多少元?![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com