
【题目】阅读下面材料:
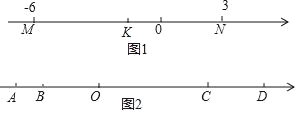
如图1,在数轴上点M表示的数是﹣6,点N表示的数是3,求线段MN的中点K所示的数.
对于求中点表示数的问题,只要用点N所表示的数3,加上点M所表示的数﹣6,得到的结果再除以2,就可以得到中点K所表示的数;即K点表示的数为![]() =﹣1.5
=﹣1.5
利用材料中知识解决下面问题:
如图2,已知数轴上有A、B、C、D四点,A点表示数为﹣6,B点表示的数是﹣4,线段AD=18,BC=3CD.
(1)点D所表示的数是 ;
(2)若点B以每秒4个单位的速度向右运动,点D以每秒1个单位的速度向左运动,同时运动t秒后,当点C为线段BD的中点时,求t的值;
(3)若(2)中点B、点D的运动速度运动方向不变,点A以每秒10个单位的速度向右运动,点C以每秒3个单位的速度向左运动,点P是线段AC的中点,点Q是线段BD的中点,A、B、C、D四点同时运动,运动时间为t,求线段PQ的长(用含t的式子表示).
【答案】(1)12;(2)![]() ;(3)线段PQ的长为2t﹣3或3﹣2t.
;(3)线段PQ的长为2t﹣3或3﹣2t.
【解析】
(1)由两点间的距离可求出AD、OA、 OD的长,在根据他们之间的关系可得D点表示的数;
(2)可求出AB、 BD、 BC 、CD、 OC即C点的坐标,由点C为线段BD的中点时,可求得t;
(2)分P点再Q点左侧和右侧两种情况讨论即可.
(1)∵AD=18,OA=6,
∴OD=18﹣6=12,
∴D点表示的数是12;
故答案为:12;
(2)∵A点表示数为﹣6,B点表示的数是﹣4,
∴AB=2,
∴BD=16,
∵BC=3CD,
∴BC=12,CD=4,
∴OC=12﹣4=8,
∴C(8,0),
由题意得:B(﹣4+4t,0),D(12﹣t,0),
∴![]() =8,
=8,
t=![]() ;
;
(3)运动后:A:﹣6+10t,
C:8﹣3t,
∴P:![]() =
=![]() ,
,
B:﹣4+4t,
D:12﹣t,
∴Q:![]() =
=![]() ,
,
当![]() ≥
≥![]() 时,t
时,t![]() ,PQ=
,PQ=![]() =2t﹣3,
=2t﹣3,
当![]() <
<![]() 时,t<
时,t<![]() ,PQ=
,PQ=![]() ﹣
﹣![]() =3﹣2t.
=3﹣2t.
综上,线段PQ的长为2t﹣3或3﹣2t.


科目:初中数学 来源: 题型:
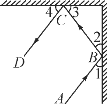
【题目】如图,一束光线在两面玻璃墙内进行传播,路径为A→B→C→D,根据光的反射性质,∠1=∠2,∠3=∠4,若∠2+∠3=90°,试探究直线AB与CD是否平行?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解) 
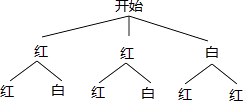
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).
(1)点C的坐标是;
(2)将△ABC沿x轴正方向平移得到△A′B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数y= ![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为 ![]() (元)、
(元)、 ![]() (元),猜想
(元),猜想 ![]() 与
与 ![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t;5辆大货车与6辆小货车一次可以运货35t
(1)每辆大货车和每辆小货车一次各可以运货多少?
(2)现在租用这两种火车共10辆,要求一次运输货物不低于30t,则大货车至少租几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?
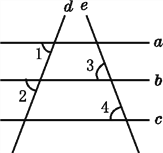
解:a与c平行.
理由:因为∠1=∠2(_________________),
所以a∥b(_________________).
因为∠3=∠4(_________________),
所以b∥c(_________________).
所以a∥c(_________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com