
【题目】正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为 .
【答案】6或2 ![]()
【解析】解: 
①如图1,点E在AD上时,
根据勾股定理得,AE= ![]() =
= ![]() =6;
=6;
②如图2,点E在CD上时,
根据勾股定理得,CE= ![]() =
= ![]() =6,
=6,
所以,DE=CD﹣CE=8﹣6=2,
在Rt△ADE中,根据勾股定理得,AE= ![]() =
= ![]() =2
=2 ![]() ,
,
综上所述,AE的长为6或2 ![]() .
.
所以答案是:6或2 ![]() .
.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过秒该直线可将平行四边形OABC的面积平分.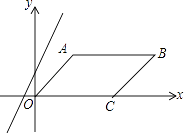
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() .
.
例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点
长度的较大值(点![]() 为垂直于
为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点![]() ,
,![]() 为
为![]() 轴上的一个动点.
轴上的一个动点.
①若点![]() (0,3),则点
(0,3),则点![]() 与点
与点![]() 的“非常距离”为 ;
的“非常距离”为 ;
②若点![]() 与点
与点![]() 的“非常距离”为2,则点
的“非常距离”为2,则点![]() 的坐标为 ;
的坐标为 ;
③直接写出点![]() 与点
与点![]() 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;
(2)已知点![]() (0,1),点
(0,1),点![]() 是直线
是直线![]() 上的一个动点,如图2,求点
上的一个动点,如图2,求点![]() 与点
与点![]() “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点![]() 的坐标.
的坐标.
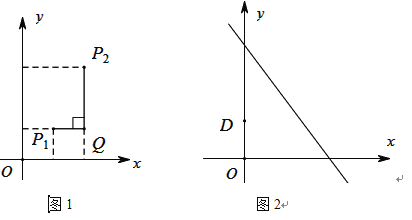
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,请分别在图1、图2中各画一条线段,各图均满足以下要求: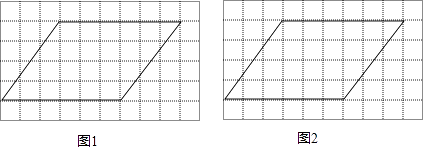
线段的一个端点为平行四边形的顶点,另一个端点在平行四边形一边的格点上(每个小正方形的顶点均为格点);
将平行四边形分割成两个图形,图1、图2中的分法各不相同,但都要求其中一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.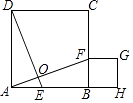
(1)判断四边形BFGH的形状并证明;
(2)写出图中所有面积相等的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意结合图形填空:如图,

点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() ,
,![]() .试说明:
.试说明:![]() ∥
∥![]() .将过程补充完整.
.将过程补充完整.
解:∵![]() (已知)
(已知)
且![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴ ∥ ( )
∴![]() ( )
( )
又∵![]() (已知)
(已知)
∴ = (等量代换 )
∴![]() ∥
∥![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“PM2.5”指数是空气中可入肺颗粒物的含量,是空气质量的指标之一.下表为A市1﹣12月“PM2.5月平均指数”(单位:微克/立方米)
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
(1)求这12个月“PM2.5月平均指数”的众数、中位数、平均数;
(2)根据《环境空气质量标准》,宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”,请你判断A市是否为宜居城市?
查看答案和解析>>
科目:初中数学 来源: 题型:
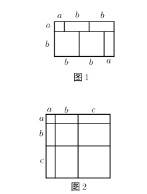
【题目】如图1,小明用1张边长为![]() 的正方形,2张边长
的正方形,2张边长![]() 为的正方形,3张边长分别为
为的正方形,3张边长分别为![]() 的长方形纸片拼成一个长为
的长方形纸片拼成一个长为![]() ,宽为
,宽为![]() 的长方形,它的面积为
的长方形,它的面积为![]() ,于是,我们可以得到等式
,于是,我们可以得到等式![]()
请解答下列问题:
(1)根据图2,写出一个代数恒等式;
(2)利用(1)中所得的结论,解决下面的问题:已知![]() ,求
,求![]() 的值.
的值.
(3)小明又用4张边长为![]() 的正方形,3张边长为
的正方形,3张边长为![]() 的正方形,8张边长分别为
的正方形,8张边长分别为![]() 的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
的长方形纸片拼出一个长方形,那么该长方形的长为__________,宽为__________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com