
【题目】如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为( )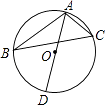
A.44°
B.34°
C.46°
D.56°
科目:初中数学 来源: 题型:
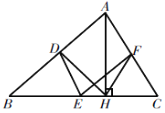
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)试判断线段DE与FH之间的数量关系,并说明理由;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.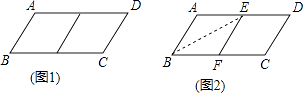
(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
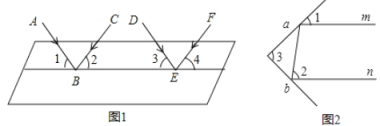
【题目】(1)阅读并回答:
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线![]() 与
与![]() 射向一个水平镜面后被反射,此时
射向一个水平镜面后被反射,此时![]() ,
,![]() .
.
①由条件可知:![]() 与
与![]() 的大小关系是____________,理由是____________;
的大小关系是____________,理由是____________;![]() 与
与![]() 的大小关系是____________;
的大小关系是____________;
②反射光线![]() 与
与![]() 的位置关系是____________,理由是____________;
的位置关系是____________,理由是____________;
(2)解决问题:
如图2,,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 镜反射,若
镜反射,若![]() 反射出的光线
反射出的光线![]() 平行于
平行于![]() ,且
,且![]() ,求
,求![]() 和
和![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.
(1)小明和小红玩摸球游戏,规定每人摸球后再将摸到的球放回去为一次游戏.若摸到黑球小明获胜,摸到黄球小红获胜,这个游戏对双方公平吗?请说明你的理由;
(2)现在裁判想从袋中取出若干个黑球,并放入相同数量的黄球,使得这个游戏对双方公平,问取出了多少黑球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com