
【题目】已知点F是等边△ABC边CA延长线上一点,点D是线段BF上一点,且BC=CD,CD交AB于点E,若AE=6,CE=14,则AF= . 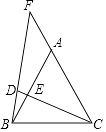
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
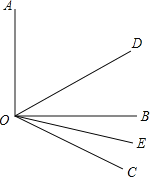
【题目】已知,如图,∠AOB=90°,∠BOC=30°,OD、OE分别是∠AOC和∠BOC的平分线.
(1)求∠COD的度数;
(2)求∠DOE的度数;
(3)若把本题的条件改成∠AOB=α,∠BOC=β,那么∠DOE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,第一次将![]() 变换成
变换成![]() ,第二次将
,第二次将![]() 变换成
变换成![]() ,第三次将
,第三次将![]() 变换成
变换成![]() ,已知:
,已知:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
![]() 、
、![]() .若将
.若将![]() 进行了
进行了![]() (
(![]() ,且
,且![]() 为整数)次变换,得到
为整数)次变换,得到![]() ,推测
,推测![]() 的坐标是_____,
的坐标是_____,![]() 点的坐标是_______.
点的坐标是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() .
.
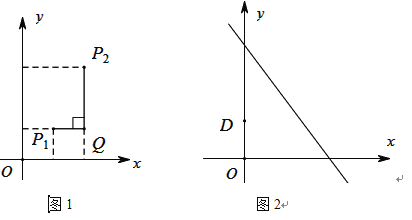
例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点
长度的较大值(点![]() 为垂直于
为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点![]() ,
,![]() 为
为![]() 轴上的一个动点.
轴上的一个动点.
①若点![]() (0,3),则点
(0,3),则点![]() 与点
与点![]() 的“非常距离”为 ;
的“非常距离”为 ;
②若点![]() 与点
与点![]() 的“非常距离”为2,则点
的“非常距离”为2,则点![]() 的坐标为 ;
的坐标为 ;
③直接写出点![]() 与点
与点![]() 的“非常距离”的最小值为 ;
的“非常距离”的最小值为 ;
(2)已知点![]() (0,1),点
(0,1),点![]() 是直线
是直线![]() 上的一个动点,如图2,求点
上的一个动点,如图2,求点![]() 与点
与点![]() “非常距离”的最小值及相应的点
“非常距离”的最小值及相应的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A'B'OC'.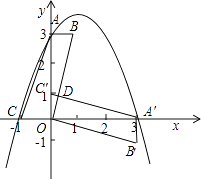
(1)若抛物线过点C,A,A',求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A'B'OC'重叠部分△OC'D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA'的面积最大?最大面积是多少?并求出此时M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,请分别在图1、图2中各画一条线段,各图均满足以下要求: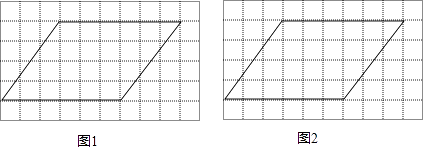
线段的一个端点为平行四边形的顶点,另一个端点在平行四边形一边的格点上(每个小正方形的顶点均为格点);
将平行四边形分割成两个图形,图1、图2中的分法各不相同,但都要求其中一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.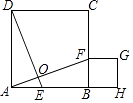
(1)判断四边形BFGH的形状并证明;
(2)写出图中所有面积相等的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A,B的坐标分别是(a,0),(b,0)且![]() .
.
(1)求点A,B的坐标;
(2)在y轴上是否存在点C,使△ABC的面积是15?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴负半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴方向以每秒2个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为18个平方单位?求此时点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com