
【题目】如图,![]() 是一个锐角三角形,分别以
是一个锐角三角形,分别以![]() 、
、![]() 向外作等边三角形
向外作等边三角形![]() 、
、![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() .
.
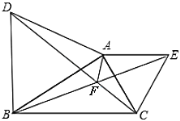
(1)求证:![]()
(2)求证:![]()
【答案】(1)见解析;(2)见解析
【解析】
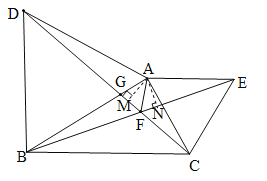
(1)过A作AM⊥CD于M,AN⊥BE于N,设AB与CD相交于点G.根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,根据全等三角形的判定定理即可得△ACD≌△AEB,根据全等三角形的性质可得AM=AN,根据角平分线的判定定理即可得到∠DFA=∠AFE,再根据全等三角形的对应角相等和三角形内角和等于180°得到∠DFB=∠DAG=60°,即可得到结论;
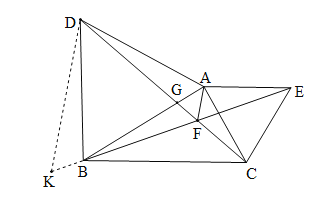
(2)如图,延长FB至K,使FK=DF,连DK,根据等边三角形的性质和全等三角形的判定和性质定理即可得到结论.
(1)过A作AM⊥CD于M,AN⊥BE于N,设AB与CD相交于点G.
∵△ABD和△ACE为等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠DAC=∠BAE=60°+∠BAC.
在△ACD和△AEB中,∵ ,
,
∴△ACD≌△AEB,
∴CD=BE,∠ADG=∠ABF,△ADC的面积=△ABE的面积,
∴![]() CDAM=
CDAM=![]() BEAN,
BEAN,
∴AM=AN,
∴AF是∠DFE的平分线,
∴∠DFA=∠AFE.
∵∠ADG=∠ABF,∠AGD=∠BGF,
∴∠DFB=∠DAG=60°,
∴∠GFE=120°,
∴∠BFD=∠DFA=∠AFE.
(2)如图,延长FB至K,使FK=DF,连接DK.
∵∠DFB=60°,
∴△DFK为等边三角形,
∴DK=DF,∠KDF=∠K=60°,
∴∠K=∠DFA=60°.
∵∠ADB=60°,
∴∠KDB=∠FDA.
在△DBK和△DAF中,
∵∠K=∠DFA,DK=DF,∠KDB=∠FDA,
∴△DBK≌△DAF,
∴BK=AF.
∵DF=DK=FK=BK+BF,
∴DF=AF+BF,
又∵CD=DF+CF,
∴CD=AF+BF+CF.


科目:初中数学 来源: 题型:
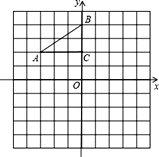
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
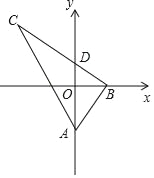
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一个学校的运动俱乐部里面有三大筐数量相同的球,甲每次从第一个大筐中取出9个球;乙每次从第二个大筐中取出7个球;丙则是每次从第三个大筐中取出5个球.到后来甲、乙、丙三人都记不清各自取过多少次球了,于是管理人员查看发现第一个大筐中还剩下7个球,第二个大筐还剩下4个球,第三个大筐还剩下2个球,那么根据上述情况可以推知甲至少取了______次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
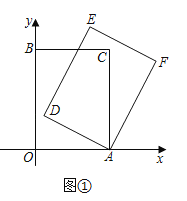
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
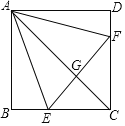
A. ①③B. ②④C. ①③④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com