
����Ŀ����ͼ1��һ����ֱ�Ĺ�·����A��B��C���أ�B��C�������150ǧ�ף��ס������������ֱ�
��B��C����ͬʱ�������ع�·ʼ������������У��ֱ�ʻ��C��B����. �ס���������A�صľ���y1��y2��ǧ�ף�����ʻʱ��x��ʱ���Ĺ�ϵ��ͼ2��ʾ��
��1������ͼ1�б��A�ص�λ�ã���д����Ӧ�ľ��룺AB= km��AC= km��
��2����ͼ2������׳�����C�ص�ʱ��a�����ֱ�д���׳�����A��֮ǰy1����ʻʱ��x�Ĺ�ϵʽ�ͼ׳���A���뿪��C�ص�y1����ʻʱ��x�Ĺ�ϵʽ(����Ҫд�Ա�����ȡֵ��Χ)��
��3���ס������������жԽ������Խ�����15ǧ��֮�ڣ���15ǧ�ף�ʱ�ܹ�����ͨ���������������öԽ���ͨ����ʱ�乲�ж��


���𰸡���1��60��90����2����B��A�� ![]() ����A��C��
����A��C�� ![]() ����3��
����3��![]()
�������������������1����ͼ�ڵã�AB=60km����AC=90km����AB��AC=2��3���ݴ˻�ͼ��
��2�����ݣ�1��0������0��60����y1����ʻʱ��x�ĺ�����ϵʽ��������ٶ�Ϊ60km/h��
�����������ȫ�̵�ʱ��Ϊ��150��60=2.5�����ݣ�1��0������2.5��90�����߶Σ�
��3���ֱ���DM��MC��BC�Ľ���ʽ������������A��С�ڵ���15kmʱ��Ӧ��ʱ�䣬������ʱ���ɣ�
���������(1)

��ͼ�٣�����AB:AC=2:3����AB=60km����AC=90km��

(2)��0<x<1.2ʱ,��AB�Ľ���ʽΪ��y1=kx+b��
��(1,0)��(0,60)����ã� ![]() ��
��
��ã� ![]() ��
��
��y1=60x+60��
���ٶ�Ϊ��60��1=60��
��150��60=2.5��
��ͼ����ʾ������׳�����C�صĺ���ͼ��
ͬ��BC�Ľ���ʽΪ��y1=60x60��
(3)DM�Ľ���ʽΪ��y2=75x+90��
ME�Ľ���ʽΪ��y2=75x90��
������ã� ![]() ��
��
��ã�34x54��
������ã� ![]() ��
��
��ã�1x75��
��1x54��
541=14��
����������ͬʱ��ָ�������öԽ���ͨ����ʱ��14Сʱ=15���ӡ�


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��20�㣬��BOC��30�㣬���AOC�Ķ��������н����ȷ����(�� ��)
A. 50�� B. 10�� C. 50���10�� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ԭ�������3�ĵ��ʾ������(�� ��)
A. 3 B. ��3 C. ��3 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е���ʽ�У���2xy��ͬ�������(����)
A. 2x2y2 B. 3y C. xy D. 4x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=-x2+bx+c��ֱ��y=![]() x+2����C��D���㣬���е�C��y���ϣ���D������Ϊ��3��
x+2����C��D���㣬���е�C��y���ϣ���D������Ϊ��3��![]() ������P��y���Ҳ����������һ���㣬����P��PE��x���ڵ�E����CD�ڵ�F��
������P��y���Ҳ����������һ���㣬����P��PE��x���ڵ�E����CD�ڵ�F��

��1���������ߵĽ���ʽ��
��2������P�ĺ�����Ϊm����mΪ��ֵʱ����O��C��P��FΪ������ı�����ƽ���ı��Σ���˵�����ɣ�
��3�������ڵ�P��ʹ��PCF=45�㣬��ֱ��д����Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽�����꼶1000��ѧ�������彡��������Ӹ��꼶�����ȡ��������ѧ���������ǰ����أ���Ϊ��������λ��kg���ֳ����飨A��39.5��46.5��B��46.5��53.5��C��53.5��60.5��D��60.5��67.5��E��67.5��74.5����������ͳ�����ݻ��������������в�������ͳ��ͼ��

����������⣺
��1����γ������������������ ������ȫƵ���ֲ�ֱ��ͼ��
��2��C��ѧ����Ƶ��Ϊ ��������ͳ��ͼ��D���Բ�Ľ��� �ȣ�
��3��������Ƹ�У�����꼶���س���60kg��ѧ����Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. ��2x2y3xy2=��6x2y2 B. ����x��2y����x+2y��=x2��4y2
C. 6x3y2��2x2y=3xy D. ��4x3y2��2=16x9y4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ѡ�ABC����ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ���A��B��C����
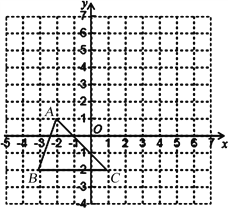
��д��A�䡢B�䡢C�������ꣻ
�������ABC�������
�ǵ�P��y���ϣ��ҡ�BCP���ABC�������ȣ����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com