
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
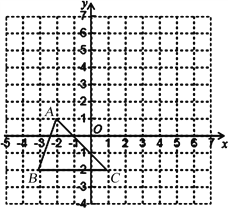
⑴写出A′、B′、C′的坐标;
⑵求出△ABC的面积;
⑶点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
【答案】(1)A′(0,4)、B′(﹣1,1)、C′(3,1);(2)S△ABC=6;(3)(0,1)或(0,﹣5).
【解析】试题分析:(1)根据横坐标右移加,左移减,纵坐标上移加,下移减即可得出三个顶点的坐标; (3)由图可知△ABC底边为4,高为3,利用面积公式求解即可;(4)设点P的坐标为(0,y),根据△BCP的面积等于△ABC的面积,列出方程![]() |y+2|×4=6,解方程即可.
|y+2|×4=6,解方程即可.
试题解析:(1)如图所示:A′(0,4)、B′(﹣1,1)、C′(3,1);
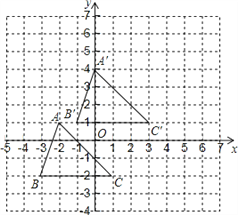
(2)S△ABC=![]() ×(3+1)×3=6;
×(3+1)×3=6;
(3)设点P坐标为(0,y),
∵BC=4,点P到BC的距离为|y+2|,
由题意得![]() ×4×|y+2|=6,
×4×|y+2|=6,
解得y=1或y=﹣5,
所以点P的坐标为(0,1)或(0,﹣5).


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图1,一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别
从B、C两地同时出发,沿公路始终匀速相向而行,分别驶往C、B两地. 甲、乙两车与A地的距离y1、y2(千米)与行驶时间x(时)的关系如图2所示:
(1)请在图1中标出A地的位置,并写出相应的距离:AB= km,AC= km;
(2)在图2中求出甲车到达C地的时间a,并分别写出甲车到达A地之前y1与行驶时间x的关系式和甲车从A地离开到C地的y1与行驶时间x的关系式(不需要写自变量的取值范围);
(3)甲、乙两车都配有对讲机,对讲机在15千米之内(含15千米)时能够互相通话,请问两车能用对讲机通话的时间共有多长?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y=![]() (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是( )
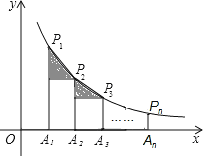
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
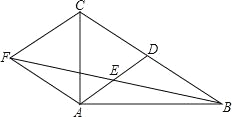
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的坐标为_______.
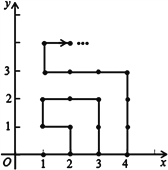
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A. 2![]() cm B. 3
cm B. 3![]() cm C. 4
cm C. 4![]() cm D. 3cm
cm D. 3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
⑴求a、b的值;
⑵若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
⑶如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.
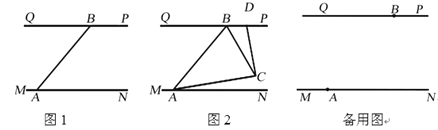
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com