
【题目】在△ABC中,∠A![]() 90°,AB
90°,AB![]() AC.
AC.
(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“![]() ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);
(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB![]()
![]() PA.
PA.
①如图2,点P在△ABC内,∠ABP![]() 30°,求∠PAB的大小;
30°,求∠PAB的大小;
②如图3,点P在△ABC外,连接PC,设∠APC![]() α,∠BPC
α,∠BPC![]() β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.

【答案】(1)否;(2)①45°;②![]() .
.
【解析】试题分析:
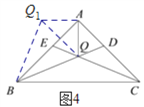
(1)如图4,把△AQC顺时针旋转90°得到△AQ1B,连接QQ1,则由题意易得QQ1=![]() AQ,由已知条件可证∠BQ1Q
AQ,由已知条件可证∠BQ1Q![]() ∠Q1BQ,从而可得BQ
∠Q1BQ,从而可得BQ![]() QQ1=
QQ1=![]() AQ;
AQ;
(2)①如图5,过点PD⊥AB于点,结合∠ABP=30°可得PD=![]() PB,结合PB=
PB,结合PB=![]() PA可得PD=
PA可得PD=![]() PA,由此即可得到sin∠PAB=
PA,由此即可得到sin∠PAB=![]() ,结合∠PAB是锐角即可得到∠PAB=45°;
,结合∠PAB是锐角即可得到∠PAB=45°;
②如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,由此可得PD=![]() PA,结合PB=
PA,结合PB=![]() PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2=
PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2= ![]() ,可得∠1+∠3=90°-
,可得∠1+∠3=90°- ![]() =∠ADP=45°,变形即可得到:
=∠ADP=45°,变形即可得到: ![]() .
.
试题解析:
(1)如图4,把△AQC绕点A顺时针旋转90°得到△AQ1B,连接QQ1,
由旋转的性质可得:AQ1=AQ,∠Q1AQ=90°,
∴QQ1=![]() AQ,
AQ,
∵BQ、CQ分别平分∠ABC、∠ACB,
∴AQ平分∠BAC,
∴∠AQ1C=∠AQC=112.5°,
∴∠BQ1Q=112.5°-45°=67.5°,
∵∠Q1BQ=45°,
∴∠Q1BQ![]() ∠BQ1Q,
∠BQ1Q,
∴BQ![]() Q1Q=
Q1Q=![]() AQ.
AQ.
故答案为:“否”;
(2)① 如图5,作PD⊥AB于D,则∠PDB=∠PDA=90°,

∵ ∠ABP=30°,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵∠PAB是锐角,
∴∠PAB=45°.
②![]() ,理由如下:
,理由如下:
如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,
∴![]() ,∠ADP=∠APD=45°.
,∠ADP=∠APD=45°.
又∵![]() ,
,
∴ PD=PB=CD.
∴ ∠DCP=∠DPC.
∵ ∠APC![]() α,∠BPC
α,∠BPC![]() β,
β,
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个30°角”的尺规作图过程.
已知:平面内一点A.
求作:∠A,使得∠A![]() 30°.
30°.
作法:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;
 (3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
∠DAB即为所求的角.
请回答:该尺规作图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.

小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(个) | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x之间的函数关系式,并画出图象;
(2)设经营此贺卡的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(t,0)是x轴上的动点,Q(0,2t)是y轴上的动点.若线段PQ与函数y=﹣|x|2+2|x|+3的图象只有一个公共点,则t的取值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
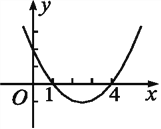
【题目】已知二次函数y=ax2-5x+c的图象如图所示.
(1)试求该二次函数的解析式和它的图象的顶点坐标;
(2)观察图象回答,x何值时y的值大于0?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com