
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)、求出将材料加热时,y与x的函数关系式;
(2)、求出停止加热进行操作时,y与x的函数关系式;
(3)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么操作时间是多少?
【答案】(1)、y=9x+15;(2)、y=![]() ;(3)、15分钟
;(3)、15分钟
【解析】
试题分析:(1)、设一次函数解析式为y=kx+b,将(0,15)和(5,60)代入一次函数解析式求出k和b的值;(2)、设反比例函数的解析式为y=![]() ,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
,将(5,60)代入求出函数解析式;(3)、将y=15代入反比例函数解析式求出x的值,然后再减去5分钟就是操作的时间.
试题解析:(1)、设函数解析式为y=kx+b 将(0,15)和(5,60)代入函数解析式可得:![]()
解得:![]() ∴一次函数的解析式为:y=9x+15
∴一次函数的解析式为:y=9x+15
、设反比例函数的解析式为:y=![]() 将(5,60)代入得:k=300 则反比例函数解析式为:y=
将(5,60)代入得:k=300 则反比例函数解析式为:y=![]() .
.
、将y=15代入反比例函数解析式可得:x=20 20-5=15(分钟)
即操作时间为15分钟.


科目:初中数学 来源: 题型:
【题目】某校体育期末考核“立定跳远”、“800米”、“仰卧起坐”三项,并按3: 5:2的比重算出期末成绩.已知小林这三项的考试成绩分别为80分、90分、100分,则小林的体育期末成绩为分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取1 000名学生的数学成绩,下列说法正确的是( )
A. 2013年昆明市九年级学生是总体 B. 每一名九年级学生是个体
C. 1 000名九年级学生是总体的一个样本 D. 样本容量是1 000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
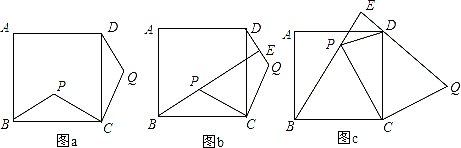
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哥哥与弟弟玩一个游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,将标有数字的一面朝下,哥哥从中任意抽取一张,记下数字后放回洗匀,然后弟弟从中任意抽取一张,计算抽得的两个数字之和,若和为奇数,则弟弟胜;若和为偶数,则哥哥胜,该游戏对双方____.(填“公平”或“不公平”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“十一”长假某湿地公园迎来旅游高峰,第一天的游客人数是1.2万人,第三天的游客人数为2.3万人,假设每天游客增加的百分率相同且设为x,则根据题意可列方程为( )
A. 2.3 (1+x)2=1.2 B. 1.2(1+x)2=2.3
C. 1.2(1﹣x)2=2.3 D. 1.2+1.2(1+x)+1.2(1+x)2=2.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:31=3,32=9,33=27,34=81,35=243,36=729,…,通过观察,用你所发现的规律确定32014的个位数字是( )
A. 3 B. 9 C. 7 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com