
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
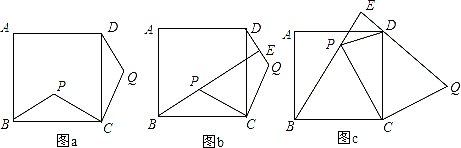
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
【答案】(1)、证明过程见解析;(2)、①、证明过程见解析;②、等腰直角三角形,证明过程见解析.
【解析】
试题分析:(1)、根据正方形性质得出BC=DC,根据旋转图形的性质得出CP=CQ以及∠PCB=∠QCD,从而得出三角形全等;(2)、①、根据全等得出∠PBC=∠QBC,设BE和CD交点为M,根据对顶角得出∠DME=∠BMC,从而说明BE⊥QD;②、根据等边三角形的性质得出PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,则∠PCD=30°,根据BC=DC,CP=CQ得出△PCD为等腰三角形,然后根据△DCQ为等边三角形,从而得出∠DEP=90°,从而得出答案.
试题解析:(1)、∵四边形ABCD是正方形,∴BC=DC
又∵将线段CP绕点C顺时针旋90°得到线段CQ,∴CP=CQ,∠PCQ=90°∴∠PCD+∠QCD=90°
又∵∠PCB+∠PCD=90° ∴∠PCB=∠QCD
在△BCP和△DCQ中 BC=DC,CP=CQ,∠PCB=∠QCD ∴△BCP≌△DCQ
(2)、①∵△BCP≌△DCQ ∴∠PBC=∠QBC
设BE和CD交点为M ∴∠DME=∠BMC ∠MED=∠MCB=90°∴BE⊥QD
②△DEP为等腰直角三角形,
∵△BOP为等边三角形 ∴PB=PC=BC ∠PBC=∠BPC=∠PCB=60°
∴∠PCD=90°-60°=30°∴∠DCQ=90°-60°=30°
又∵BC=DC CP=CQ∴PC=DC DC=CQ ∴△PCD是等腰三角形
△DCQ是等边三角形 ∴∠CPD=∠CDP=75°∠CDQ=60°∴∠EPD=180°-15°-60°=45°
∠EDP=180°-75°-60°=45 °∴∠EPD=∠EDP PE=DE ∴∠DEP=180°-45°-45°=90°
∴△DEP是等腰直角三形


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在CCTV“开心辞典”栏目中,主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套. 经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)、学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
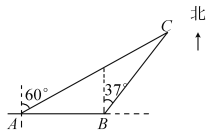
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)、求出将材料加热时,y与x的函数关系式;
(2)、求出停止加热进行操作时,y与x的函数关系式;
(3)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么操作时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1∶![]() ,点P、H、B、C、A在同一平面上,点H、B、C在同一条直线上,且PH⊥HC,
,点P、H、B、C、A在同一平面上,点H、B、C在同一条直线上,且PH⊥HC,
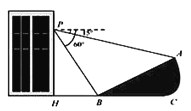
(1)山坡坡角(即∠ABC)的度数等于 度.
(2)求A、B两点间的距离(结果精确到0.1米.参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com