
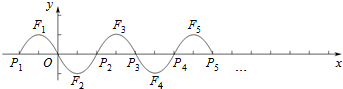
分析 根据抛物线的解析式来求F1的顶点坐标;根据该“波浪抛物线”顶点坐标纵坐标分别为1和-1即可得出结论.
解答 解:∵y=-x2-2x=-(x+1)2+1,
∴F1的顶点坐标为 (-1,1).
又y=-x2-2x=-x(x+2),
∴P1(-2,0),
∴根据函数的对称性得到:F2的顶点坐标为(1,-1),P2(2,0),
F3的顶点坐标为(3,1),P3(4,0),
…
F8的顶点坐标为(13,-1),
Fn的顶点坐标为[2n-3,(-1)n+1].
故答案是:(-1,1);(13,-1);[2n-3,(-1)n+1].
点评 本题考查了二次函数图象与几何变换.解题的关键是找到Fn的顶点坐标变换规律.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
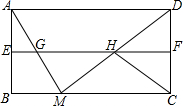 如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com