
 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,分析 (1)先把A点的横坐标代入一次函数中可确定A点坐标,然后把A点坐标代入反比例函数解析式中可计算出k的值;
(2)根据S△AOC=S△CON+S梯形AMNC-S△AOM=S梯形AMNC即可求得.
(3)由题意可知A,B两点关于原点对称,从而得到点B的坐标,根据对角线互相平分的四边形是平行四边形可得S△APB=3,根据两点间的距离公式可得AB的长度,进而得到点P到直线AB的距离,设出点P的坐标根据点到直线的距离公式即可求得点P的坐标.
解答 解:(1)把x=2代入y=$\frac{1}{2}$x得y=$\frac{1}{2}$×2=1,
所以A点坐标为(2,1),把A(2,1)代入y=$\frac{k}{x}$得1=$\frac{k}{2}$,
解得k=2;
(2)如图1, 把y=4代入y=$\frac{2}{x}$得4=$\frac{2}{x}$,解得x=$\frac{1}{2}$,
把y=4代入y=$\frac{2}{x}$得4=$\frac{2}{x}$,解得x=$\frac{1}{2}$,
作AM⊥x轴于M,CN⊥x轴于N,
∵S△AOC=S△CON+S梯形AMNC-S△AOM,S△CON=S△AOM=$\frac{1}{2}$|k|,
∴S△AOC=S梯形AMNC=$\frac{1}{2}$(4+1)(2-$\frac{1}{2}$)=$\frac{15}{4}$;
(3)如图2,∵A(2,1),反比例函数的图象关于原点对称,
∴点A,B,P,Q为顶点组成的四边形为平行四边形,点B的坐标为(-2,-1),
过A作y轴的平行线,过B作x轴的平行线,两线交于D,
AD=2,BD=4,
∴AB=2$\sqrt{5}$,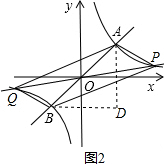
∵四边形APBQ面积是6,
∴S△APB=3,
∴P到AB距离=$\frac{3\sqrt{5}}{5}$,
∵P在双曲线上,
设P(x,$\frac{2}{x}$),
根据点到直线距离公式,d=$\frac{|x-\frac{4}{x}|}{\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$,
∴x=4或者x=-1(舍去)或者x=-4(舍去)或者x=1;
所以P(4,$\frac{1}{2}$)或者P(1,2).
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数与正比例函数的交点关于原点对称;反比例函数的比例系数等于在它上面的点的横纵坐标的积,三角形面积公式以及点到直线的距离公式等知识点.


科目:初中数学 来源: 题型:解答题
 如图,已知扇形AOB中,∠AOB=120°,弦AB=2$\sqrt{3}$,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M,分别过点A、B作⊙M的切线,两切线相交于点C.
如图,已知扇形AOB中,∠AOB=120°,弦AB=2$\sqrt{3}$,点M是弧AB上任意一点(与端点A、B不重合),ME⊥AB于点E,以点M为圆心、ME长为半径作⊙M,分别过点A、B作⊙M的切线,两切线相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
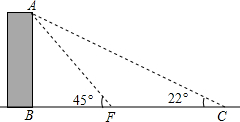 如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)
如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
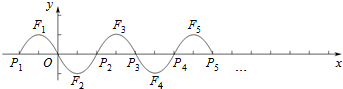
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com