
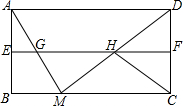
 如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.分析 (1)利用平行四边形的判定方法得出四边形AEFD是平行四边形,进而利用平行四边形的性质得出答案;
(2)利用平行四边形的判定方法一组对边平行且相等的四边形是平行四边形得出即可;
(3)利用当a=$\frac{\sqrt{3}}{2}$b时,由题意得出MC=BM=$\frac{1}{2}$b,AM=b,则MG=$\frac{1}{2}$b,进而利用(2)中所求得出答案.
解答 (1)解:GH=$\frac{1}{2}$b,是定值,
理由:∵E,F分别是AB,CD的中点,
∴AE∥DF且AE=DF,
∴四边形AEFD是平行四边形,
∴AD∥EF∥BC,
∴$\frac{AG}{MG}$=$\frac{AE}{BE}$=$\frac{DH}{MH}$,
∴AG=MG,DH=MH,
∴GH=$\frac{1}{2}$AD=$\frac{1}{2}$b,是定值;
(2)证明:∵点M为BC的中点,
∴MC=$\frac{1}{2}$BC=$\frac{1}{2}$b,
∵GH=$\frac{1}{2}$b,
∴GH=CM,
又∵GH∥CM,
∴四边形GMCH是平行四边形;
(3)解:a=$\frac{\sqrt{3}}{2}$b时,四边形GMCH是菱形.
点评 此题主要考查了菱形的判定以及平行四边形的判定与性质,熟练应用平行四边形的判定方法是解题关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
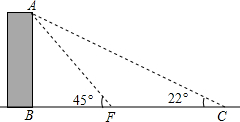 如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)
如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
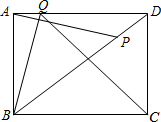 如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
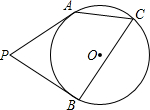 如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )
如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a-c>-b-c | D. | -a<-b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com