
分析 (1)将点A和点B的坐标代入抛物线的解析式得到关于a、b的方程组,然后求得a、b的值即可;
(2)过点N作NM⊥x轴点M,则∠AMN=90°.设点N的坐标为(x,$\frac{3}{4}$x2-$\frac{9}{4}$x-3),则AM=x+1,MN=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3,然后依据tan∠BAN=2,列方程求解即可;
(3)连接CD,过点C作CG⊥AD,垂足为G,过点D作DF⊥x轴,垂足为F.先求得AC,AD的长,依据S△ACD=$\frac{1}{2}$CD•OC=$\frac{1}{2}$AD•CG,可求得CG的长,然后依据勾股定理可求得AG的长,从而可得到tan∠AED=$\frac{DF}{EF}$=$\frac{DF}{E′F}$=$\frac{9}{13}$,从而可求得EF和E′F的长,然后求得点E和点E′的坐标即可;
(4)先证明AB=BC,由等腰三角形的性质可知MB为AC的垂直平分线,然后再证明△CMP∽△F′MC,依据相似三角形的性质可求得MP•MF′=$\frac{5}{2}$,最后由m=S1•S2=$\frac{1}{2}$AC•PM•$\frac{1}{2}$AC•MF′求解即可.
解答 解:(1)将点A和点B的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{a-b-3=0}\\{16a+4b-3=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=-\frac{9}{4}}\end{array}\right.$.
∴抛物线的解析式为y=$\frac{3}{4}$x2-$\frac{9}{4}$x-3.
(2)如图1所示:过点N作NM⊥x轴点M,则∠AMN=90°.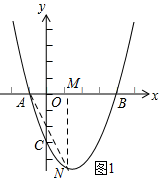
设点N的坐标为(x,$\frac{3}{4}$x2-$\frac{9}{4}$x-3),则AM=x+1,MN=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.
∵tan∠BAN=2,
∴$\frac{-\frac{3}{4}{x}^{2}+\frac{9}{4}x+3}{x+1}$=2,解得:x=$\frac{4}{3}$或x=-1(舍去).
∴MN=2AM=3×($\frac{4}{3}$+1)=$\frac{14}{3}$,
∴点N的坐标为($\frac{4}{3}$,-$\frac{14}{3}$).
(3)如图2所示:连接CD,过点C作CG⊥AD,垂足为G,过点D作DF⊥x轴,垂足为F.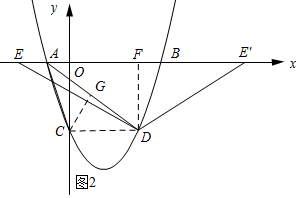
∵点C与点D关于对称轴直线x=$\frac{3}{2}$对称,
∴D(3,-3).
∴DF=3,CD=3.
依据两点间的距离公式可知AD=5,AC=$\sqrt{10}$.
∵S△ACD=$\frac{1}{2}$CD•OC=$\frac{1}{2}$AD•CG,
∴CG=$\frac{9}{5}$.
∴AG=$\sqrt{A{C}^{2}-C{G}^{2}}$=$\frac{13}{5}$.
∴tan∠CAD=$\frac{9}{13}$.
∵∠AED=∠CAD,
∴tan∠AED=$\frac{DF}{EF}$=$\frac{DF}{E′F}$=$\frac{9}{13}$,即$\frac{3}{E′F}$=$\frac{3}{EF}$=$\frac{9}{13}$,解得EF=EF′=$\frac{13}{3}$.
∴E(-$\frac{4}{3}$,0),E′($\frac{22}{3}$,0).
∴点E的坐标为(-$\frac{4}{3}$,0)或($\frac{22}{3}$,0).
(4)如图3所示: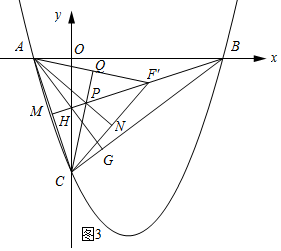
∵A(-1,0),(4,0),C(0,-3),
∴AB=BC=5,AC=$\sqrt{10}$.
∵MB为△ABC的中线,
∴MB⊥AC,MC=$\frac{\sqrt{10}}{2}$.
∴MB为AC的垂直平分线,
∴∠AF′M=∠CF′M.
∵点P为AF′与CF′的高线的交点,
∴∠CAQ+∠ACQ=90°,∠CAQ+∠MF′A=90°,
∴∠ACQ=∠AF′M.
∴∠ACQ=∠CF′M.
又∵∠CMP=∠CMF′,
∴△CMP∽△F′MC.
∴$\frac{MP}{MC}$=$\frac{MC}{F′M}$,即MP•MF′=$\frac{5}{2}$.
∴m=S1•S2=$\frac{1}{2}$AC•PM•$\frac{1}{2}$AC•MF′=$\frac{1}{4}$×($\sqrt{10}$)2×$\frac{5}{2}$=$\frac{25}{4}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,锐角三角函数的定义、三角形的面积、等腰三角形的性质和判定、相似三角形的性质和判定,求得tan∠AED的值是解答问题(3)的关键;求得MP•MF′=$\frac{5}{2}$是解答问题(4)的关键.


科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x>1且x≠2 | C. | x≥1且x≠2 | D. | x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间第x(天) | 1≤x<30 | 30≤x≤50 |
| 售价(元/件) | x+30 | 60 |
| 每天销量(件) | 100-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
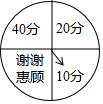 “五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com