
【题目】如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )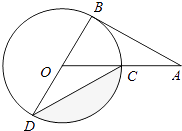
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如图,过O点作OE⊥CD于E,
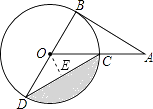
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵OA=2,
∴⊙O的半径为1,
∴OE= ![]() ,CE=DE=
,CE=DE= ![]() ,
,
∴CD=2CE=2× ![]() =
= ![]() ,
,
∴S阴影=S扇形COD﹣S△COD= ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]() ,
,
所以答案是:A.
【考点精析】通过灵活运用切线的性质定理和扇形面积计算公式,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
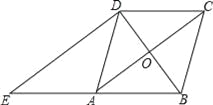
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
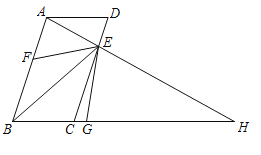
【题目】如图,![]() ,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得
,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得![]() ,作
,作![]() 的角平分线
的角平分线![]() 交BH于点G,若
交BH于点G,若![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
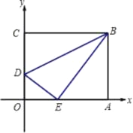
【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:
对于两个不等的非零实数a、b,若分式![]() 的值为零,则x=a或x=b.又因为
的值为零,则x=a或x=b.又因为![]() =
=![]() ,所以关于x的方程x+
,所以关于x的方程x+![]() =a+b有两个解,分别为x1=a,x2=b.
=a+b有两个解,分别为x1=a,x2=b.
应用上面的结论解答下列问题:
(1)方程x+![]() =q的两个解分别为x1=﹣1、x2=4,则P= ,q= ;
=q的两个解分别为x1=﹣1、x2=4,则P= ,q= ;
(2)方程x+![]() =4的两个解中较大的一个为 ;
=4的两个解中较大的一个为 ;
(3)关于x的方程2x+![]() =2n的两个解分别为x1、x2(x1<x2),求
=2n的两个解分别为x1、x2(x1<x2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
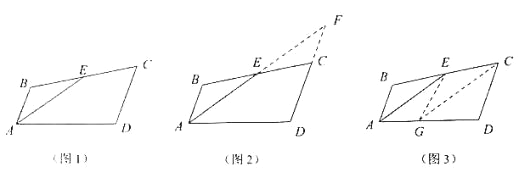
小明遇到这样一个问题:如图 1,在四边形 ABCD 中,E 是 BC 的中点,AE 是∠BAD 的平分线,AB∥DC,求证:AD=AB+DC. 小明发现以下两种方法:
方法 1:如图 2,延长 AE、DC 交于点 F;
方法 2:如图 3,在 AD 上取一点 G 使 AG=AB,连接 EG、CG.
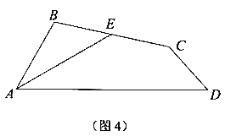
(1)根据阅读材料,任选一种方法,证明:AD=AB+DC; 用学过的知识或参考小明的方法,解决下面的问题:
(2)如图 4,在四边形 ABCD 中,AE 是∠BAD 的平分线,E 是 BC 的中点,∠BAD=60°,∠ABC=180°-![]() ∠BCD,求证:CD=CE.
∠BCD,求证:CD=CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com