
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 
(1)图中的全等三角形有;
(2)从你找到的全等三角形中选出其中一对加以证明.
【答案】
(1)△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE
(2)解:理由如下:
∵D是BC的中点,
∴BD=CD,
在△ABD和△ACD中,
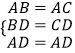 ,
,
∴△ABD≌△ACD(SSS);
∴∠BAE=∠CAE,
在△ABE和△ACE中,
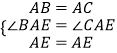 ,
,
∴△ABE≌△ACE(SAS);
∴BE=CE,
在△BDE和△CDE中,
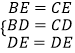 ,
,
∴△BDE≌△CDE(SSS).
故答案为:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE.
【解析】解:(1)图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
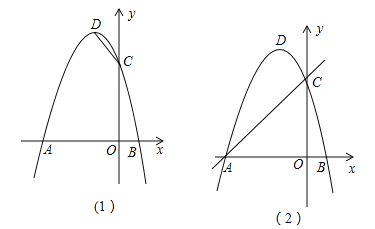
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
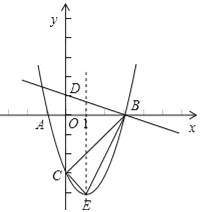
【题目】如图,抛物线![]() (a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线
(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( ) 
A.a2﹣b2=(a﹣b)2
B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2
D.a2﹣b2=(a+b)(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为迎接省运会,要将某一城市美化工程招标,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为![]() ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com