
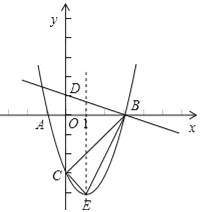
【题目】如图,抛物线![]() (a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线
(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3)P(1,﹣1)或P(1,
;(2)证明见解析;(3)P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,
)或P(1,![]() )或P(1,
)或P(1,![]() ).
).
【解析】
试题分析:(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;
(2)先求出点A,B,C,D,E的坐标,从而求出BC,BE,CE,OD,OB,BD,求出比值,得到![]() 得出结论;
得出结论;
(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
试题解析:(1)∵抛物线![]() ,∴c=﹣3,∴C(0,﹣3),∴OC=3,∵BO=OC=3AO,∴BO=3,AO=1,∴B(3,0),A(﹣1,0),∵该抛物线与x轴交于A、B两点,∴
,∴c=﹣3,∴C(0,﹣3),∴OC=3,∵BO=OC=3AO,∴BO=3,AO=1,∴B(3,0),A(﹣1,0),∵该抛物线与x轴交于A、B两点,∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)由(1)知,抛物线解析式为![]() =
=![]() ,∴E(1,﹣4),∵B(3,0),A(﹣1,0),C(0,﹣3),∴BC=
,∴E(1,﹣4),∵B(3,0),A(﹣1,0),C(0,﹣3),∴BC=![]() ,BE=
,BE=![]() ,CE=
,CE=![]() ,∵直线
,∵直线![]() 与y轴交于点D,∴D(0,1),∵B(3,0),∴OD=1,OB=3,BD=
与y轴交于点D,∴D(0,1),∵B(3,0),∴OD=1,OB=3,BD=![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,∴△BCE∽△BDO;
,∴△BCE∽△BDO;
(3)存在,理由:设P(1,m),∵B(3,0),C(0,﹣3),∴BC=![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,∵△PBC是等腰三角形,∴分三种情况讨论:
,∵△PBC是等腰三角形,∴分三种情况讨论:
①当PB=PC时,∴![]() =
=![]() ,∴m=﹣1,∴P(1,﹣1);
,∴m=﹣1,∴P(1,﹣1);
②当PB=BC时,∴![]() =
=![]() ,∴m=
,∴m=![]() ,∴P(1,
,∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() );
);
③当PC=BC时,∴![]() =
=![]() ,∴m=
,∴m=![]() ,∴P(1,
,∴P(1,![]() )或P(1,
)或P(1,![]() );
);
综上所述:符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,
)或P(1,![]() )或P(1,
)或P(1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A′B′C′关于直线m对称。
(1)结合图形指出对称点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其它对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 
(1)图中的全等三角形有;
(2)从你找到的全等三角形中选出其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4.
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com