
����Ŀ���ס��ҡ���������ɽ�����߾�����Լȥ��ɽ������1�¼ײμ������ε�ɽ���
��1��1��1�ռ�����ͬʱ��ʼ�ʵ�һ��900�ߵ�ɽ����ƽ���ʵ��ٶ����ҵ�1.2��������ױ�����15���ӵ��ﶥ�壮���ƽ���ʵ��ٶ���ÿ���Ӷ����ף�
��2��1��6�ռ����ȥ�ʵ���һ��h�ߵ�ɽ���ױ��ֵڣ�1�����е��ٶȲ��䣬�ȱ�������0.5Сʱ���������ͬʱ���ﶥ�壬�ʼ�ƽ���ʵ��ٶ��DZ��Ķ��ٱ������ú�h�Ĵ���ʽ��ʾ��
���𰸡�
��1���⣺���ҵ��ٶ�Ϊx��/���ӣ�
![]() ��
��
��ã�x=10��
�����飬x=10��ԭ��ʽ���̵Ľ⣬
��1.2x=12��
����ƽ���ʵ��ٶ���12��/���ӣ�
��2���⣺�����ƽ���ʵ��ٶ���y��/�֣�
![]() ��
��
����
y= ![]() ��
��
���ƽ���ʵ��ٶ��DZ��ģ� ![]() ����
����
����ƽ���ʵ��ٶ��DZ��� ![]() ����
����
����������1��������������г���Ӧ�ķ�ʽ���̣��Ӷ�������ü�ƽ���ʵ��ٶȣ���2�����ݣ�1���м��ٶȿ��Ա�ʾ�������ٶȣ����ü��ٶȱȱ���ƽ���ʵ��ٶȼ��ɽ���⣮
�����㾫�������÷�ʽ���̵�Ӧ�ö���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�з�ʽ���̽�Ӧ����IJ��裺���⡢��δ֪��������ȹ�ϵ�з��̡��ⷽ�̲������д���𰸣�Ҫ�е�λ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��2x2����ƽ��3����λ��������ƽ��2����λ���õ����������ǣ�������
A.y��2��x+2��2��3B.y��2��x+2��2+3
C.y��2��x��2��2��3D.y��2��x��2��2+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
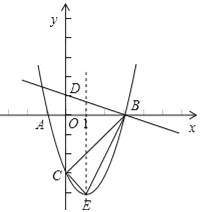
����Ŀ����ͼ��������![]() ��a��0���Ķ���ΪE������������x�ύ��A��B���㣬��y�ύ�ڵ�C����BO=OC=3AO��ֱ��
��a��0���Ķ���ΪE������������x�ύ��A��B���㣬��y�ύ�ڵ�C����BO=OC=3AO��ֱ��![]() ��y�ύ�ڵ�D��
��y�ύ�ڵ�D��
��1���������ߵĽ���ʽ��
��2��֤������DBO�ס�EBC��
��3���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PBC�ǵ��������Σ������ڣ���ֱ��д������������P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊӭ��ʡ�˻ᣬҪ��ijһ�������������б꣬�мס����������̶�Ͷ�꣬�����㣺�ӵ�������������Ҫ60�죬���ɼ�����20�죬ʣ�µĹ����ɼס��Һ���24�����ɣ�
��1���Ҷӵ�������������Ҫ�����죿
��2����ʩ��һ�죬�踶���̿�3.5��Ԫ���Ҷ�ʩ��һ���踶���̿�2��Ԫ�����ù��̼ƻ���70������ɣ��ڲ������ƻ�������ǰ���£����ɼӻ��Ҷӵ�����ɹ���ʡǮ�������ɼ�������ȫ�̺�����ɸù���ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M�������ǣ�5��4������M��y�������ڵ�C����x���ཻ��A��B���㣮
��1�����A��B��C������ֱ���A��__��__����B��__��__����C��__��__����
��2���辭��A��B����������߽���ʽΪ![]() �����Ķ���ΪF����֤��ֱ��FA����M���У�
�����Ķ���ΪF����֤��ֱ��FA����M���У�
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�P���ҵ�P��x����Ϸ���ʹ��PBC�ǵ��������Σ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�����ȷ���ǣ� ��
A.��7x=4x��3�����7x��4x=3
B.�� ![]() =1+
=1+ ![]() ȥ��ĸ��2��2x��1��=1+3��x��3��
ȥ��ĸ��2��2x��1��=1+3��x��3��
C.��2��2x��1����3��x��3��=1ȥ���ŵ�4x��2��3x��9=1
D.��2��x+1��=x+7ȥ���š�����ϲ�ͬ�����x=5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���OΪԭ�㣬��A������Ϊ����6��0������ͼ1��������OBCD�Ķ���B��x��ĸ������ϣ���C�ڵڶ����ޣ��ֽ�������OBCD�Ƶ�O˳ʱ����ת�Ǧ��õ�������OEFG��
��1����ͼ2������=60�㣬OE=OA����ֱ��EF�ĺ�������ʽ��
��2������Ϊ��ǣ�tan��=![]() ����AEȡ����Сֵʱ����������OEFG�������
����AEȡ����Сֵʱ����������OEFG�������
��3����������OEFG�Ķ���F����y����ʱ��ֱ��AE��ֱ��FG�ཻ�ڵ�P����OEP����������֮���ܷ�Ϊ![]() ��1�����ܣ����P�����ꣻ�����ܣ���˵��������
��1�����ܣ����P�����ꣻ�����ܣ���˵��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��O��B������ͬһ��ֱ���ϣ�ODƽ�֡�AOC��OEƽ�֡�BOC��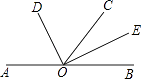
��1������BOC=62�㣬���DOE�Ķ�����
��2������BOC=a�㣬���DOE�Ķ�����
��3��ͼ���Ƿ��л���Ľǣ�������д�����л���Ľǣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com