
【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式;
(2)若α为锐角,tanα=![]() ,当AE取得最小值时,求正方形OEFG的面积;
,当AE取得最小值时,求正方形OEFG的面积;
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为![]() :1?若能,求点P的坐标;若不能,试说明理由.
:1?若能,求点P的坐标;若不能,试说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,P1(0,6),P2(﹣6,18),P3(﹣18,36),P4(﹣6,0),P5(﹣18,6).
;(3)存在,P1(0,6),P2(﹣6,18),P3(﹣18,36),P4(﹣6,0),P5(﹣18,6).
【解析】
试题分析:(1)先判断出△AEO为正三角形,再根据锐角三角函数求出OM即可;
(2)判断出当AE⊥OQ时,线段AE的长最小,用勾股定理计算即可;
(3)由△OEP的其中两边之比为![]() :1分三种情况进行计算即可.
:1分三种情况进行计算即可.
试题解析:(1)如图1,过点E作EH⊥OA于点H,EF与y轴的交点为M.
∵OE=OA,α=60°,∴△AEO为正三角形,∴OH=3,EH=![]() =
=![]() ,∴E(﹣3,
,∴E(﹣3,![]() ).
).
∵∠AOM=90°,∴∠EOM=30°.
在Rt△EOM中,∵cos∠EOM=![]() ,即
,即![]() ,∴OM=
,∴OM=![]() ,∴M(0,
,∴M(0,![]() ).
).
设直线EF的函数表达式为![]() ,∵该直线过点E(﹣3,
,∵该直线过点E(﹣3,![]() ),∴
),∴![]() =
=![]() ,解得
,解得![]() ,所以,直线EF的函数表达式为
,所以,直线EF的函数表达式为![]() .
.

(2)如图2,射线OQ与OA的夹角为α( α为锐角,tanα=![]() ).
).
无论正方形边长为多少,绕点O旋转角α后得到正方
形OEFG的顶点E在射线OQ上,∴当AE⊥OQ时,线段AE的长最小.
在Rt△AOE中,设AE=a,则OE=2a,∴![]() ,解得
,解得![]() ,
,![]() (舍去),∴OE=2a=
(舍去),∴OE=2a=![]() ,∴S正方形OEFG=
,∴S正方形OEFG=![]() =
=![]() .
.

(3)设正方形边长为m.
当点F落在y轴正半轴时.如图3,当P与F重合时,△PEO是等腰直角三角形,有![]() 或
或![]() .
.
在Rt△AOP中,∠APO=45°,OP=OA=6,∴点P1的坐标为(0,6).

在图3的基础上,当减小正方形边长时,点P在边FG 上,△OEP的其中两边之比不可能为![]() :1;
:1;
当增加正方形边长时,存在![]() (图4)和
(图4)和![]() (图5)两种情况.
(图5)两种情况.
如图4,△EFP是等腰直角三角形,有![]() =
=![]() ,即
,即![]() =
=![]() ,此时有AP∥OF.
,此时有AP∥OF.
在Rt△AOE中,∠AOE=45°,∴OE=![]() OA=
OA=![]() ,∴PE=
,∴PE=![]() OE=12,PA=PE+AE=18,∴点P2的坐标为(﹣6,18).
OE=12,PA=PE+AE=18,∴点P2的坐标为(﹣6,18).

如图5,过P作PR⊥x轴于点R,延长PG交x轴于点H.设PF=n.
在Rt△POG中,![]() =
=![]() =
=![]() ,在Rt△PEF中,
,在Rt△PEF中,![]() =
=![]() ,当
,当![]() 时,∴
时,∴![]() ,∴
,∴![]() =
=![]() ,得n=2m.
,得n=2m.
∵EO∥PH,∴△AOE∽△AHP,∴![]() ,∴AH=4OA=24,即OH=18,∴m=
,∴AH=4OA=24,即OH=18,∴m=![]() .
.
在等腰Rt△PRH中,PR=HR=![]() PH=36,∴OR=RH﹣OH=18,∴点P3的坐标为(﹣18,36).
PH=36,∴OR=RH﹣OH=18,∴点P3的坐标为(﹣18,36).

当点F落在y轴负半轴时,如图6,P与A重合时,在Rt△POG中,OP=![]() OG,又∵正方形OGFE中,OG=OE,∴OP=
OG,又∵正方形OGFE中,OG=OE,∴OP=![]() OE,∴点P4的坐标为(﹣6,0).
OE,∴点P4的坐标为(﹣6,0).

在图6的基础上,当正方形边长减小时,△OEP的其中两边之比不可能为![]() :1;当正方形边长增加时,存在
:1;当正方形边长增加时,存在![]() (图7)这一种情况.
(图7)这一种情况.
如图7,过P作PR⊥x轴于点R,设PG=n.
在Rt△OPG中,![]() =
=![]() ,在Rt△PEF中,
,在Rt△PEF中,![]() =
=![]() =
=![]() .
.
当![]() 时,∴
时,∴![]() ,∴
,∴![]() =
=![]() ,∴n=2m,由于NG=OG=m,则PN=NG=m,∵OE∥PN,∴△AOE∽△ANP,∴
,∴n=2m,由于NG=OG=m,则PN=NG=m,∵OE∥PN,∴△AOE∽△ANP,∴![]() =1,即AN=OA=6.
=1,即AN=OA=6.
在等腰Rt△ONG中,ON=![]() m,∴12=
m,∴12=![]() m,∴m=
m,∴m=![]() ,在等腰Rt△PRN中,RN=PR=6,∴点P5的坐标为(﹣18,6).
,在等腰Rt△PRN中,RN=PR=6,∴点P5的坐标为(﹣18,6).

所以,△OEP的其中两边的比能为![]() :1,点P的坐标是:P1(0,6),P2(﹣6,18),P3(﹣18,36),P4(﹣6,0),P5(﹣18,6).
:1,点P的坐标是:P1(0,6),P2(﹣6,18),P3(﹣18,36),P4(﹣6,0),P5(﹣18,6).


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB=8,BC=15,CA=17,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积是60
D.△ABC是直角三角形,且∠A=60°
查看答案和解析>>
科目:初中数学 来源: 题型:
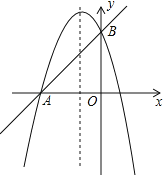
【题目】如图,已知抛物线![]() 与直线AB相交于A(﹣3,0),B(0,3)两点.
与直线AB相交于A(﹣3,0),B(0,3)两点.
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9. 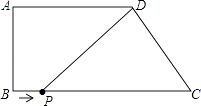
(1)求CD的长为 .
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com