
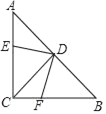
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,D为AB中点,点E,F分别在AC,BC边上,且AE=CF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
【答案】(1)详见解析;(2)∠DEF是45°.
【解析】
(1)根据直角三角形的性质和全等三角形的性质、判定可以证明结论成立;
(2)根据全等三角形的性质和直角三角线斜边上的中线等于斜边的一半、等腰三角形的性质可以求得∠DEF的度数.
(1)证明:∵AC=BC,∠ACB=90°,D为AB的中点,
∴∠A=∠DCB=45°,CD=![]() AB=AD,
AB=AD,
在△ADE和△CDF中,
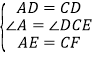 ,
,
∴△ADE≌△CDF(SAS),
∴DE=DF;
(2)∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵AC=BC,∠ACB=90°,点D为AB的中点,
∴CD⊥AB,
∴∠ADC=90°,
∴∠ADE+∠EDC=90°,
∴∠CDF+∠EDC=90°,
∴∠EDF=90°,
又∵DE=DF,
∴∠DEF=∠DFE=45°,
即∠DEF是45°.


科目:初中数学 来源: 题型:
【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程![]() ﹣
﹣![]() =1
=1
老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得![]() ×6﹣
×6﹣![]() ×6=1…………①
×6=1…………①
去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
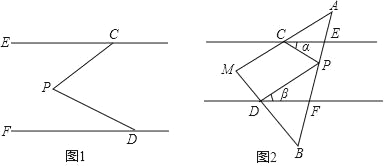
【题目】(问题探究)如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(问题迁移)
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
(1)当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
(2)如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 . 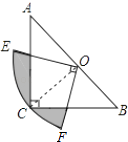
查看答案和解析>>
科目:初中数学 来源: 题型:
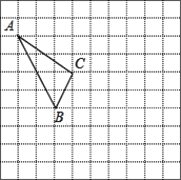
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为A(-4,5),C(-1,3).
(1)请在如图所示的网格内作出x轴、y轴;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标并求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
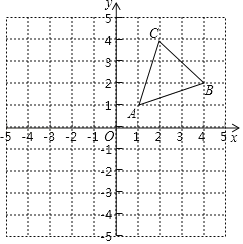
【题目】已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(2,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)①借助图中的网格,请只用直尺(不含刻度)在图中找一点P,使得P到AB、AC的距离相等,且PA=PB.
②若x轴上有一动点Q,使得△QAB的周长最小,则△QAB的最小周长为 .
(友情提醒:请别忘了标注宇母)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com