
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由

【答案】(1)点B的坐标为(3,0)或(﹣5,0);画△ABC见解析;
(2)△ABC的面积为8;
(3)点P的坐标为(0,5)或(0,﹣5)
【解析】试题分析:(1)分点B在点A的左边和右边两种情况解答;(2)利用三角形的面积公式列式计算即可得解;(3)利用三角形的面积公式列式求出点P到x轴的距离,然后分两种情况写出点P的坐标即可.
试题解析:(1)点B在点A的右边时,﹣1+4=3,点B在点A的左边时,﹣1﹣4=﹣5,
所以,B的坐标为(3,0)或(﹣5,0),
如图所示:
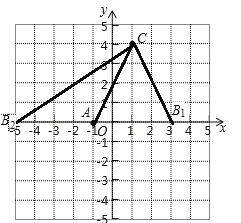
(2)△ABC的面积=![]() ×4×4=8;
×4×4=8;
(3)设点P到x轴的距离为h,则![]() ×4h=10,解得h=5,
×4h=10,解得h=5,
点P在y轴正半轴时,P(0,5),点P在y轴负半轴时,P(0,﹣5),
综上所述,点P的坐标为(0,5)或(0,﹣5).


科目:初中数学 来源: 题型:
【题目】一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BD=CE,BE=CF.

(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
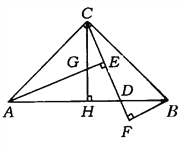
【题目】如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.
(1)试说明AH=BH
(2)求证:BD=CG.
(3)探索AE与EF、BF之间的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com