练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO=108°，则∠C的度数为（ ）

    A. 40° B. 41° C. 32° D. 36°

    【答案】D

    【解析】分析：如图，连接AO、BO．由题意EA=EB=EO，推出∠AOB=90°，∠OAB+∠OBA=90°，由DO=DA，FO=FB，推出∠DAO=∠DOA，∠FOB=∠FBO，推出∠CDO=2∠DAO，∠CFO=2∠FBO，由∠CDO+∠CFO=108°，推出2∠DAO+2∠FBO=98°，推出∠DAO+∠FBO=49°，由此即可解决问题．

    详解：如图，连接AO、BO．

    由题意得：EA=EB=EO，∴∠AOB=90°，∠OAB+∠OBA=90°．∵DO=DA，FO=FB，∴∠DAO=∠DOA，∠FOB=∠FBO，∴∠CDO=2∠DAO，∠CFO=2∠FBO．∵∠CDO+∠CFO=108°，∴2∠DAO+2∠FBO=108°，∴∠DAO+∠FBO=54°，∴∠CAB+∠CBA=∠DAO+∠OAB+∠OBA+∠FBO=144°，∴∠C=180°﹣（∠CAB+∠CBA）=180°﹣144°=36°．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，然后解决问题：

    截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．

    (1)如图①，在△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

    解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是 ；

    (2)问题解决：

    如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE＋CF＞EF；

    (3)问题拓展：

    如图③，在四边形ABCD中，∠B＋∠D＝180°，CB＝CD，∠BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：

    摸球的次数n

    100

    150

    200

    500

    800

    1000

    摸到白球的次数m

    58

    96

    116

    295

    484

    601

    摸到白球的频率

    0.58

    0.64

    0.58

    0.59

    0.605

    0.601

    （1）请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）

    （2）试估算口袋中白种颜色的球有多少只？

    （3）请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球；这两只球颜色不同的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ABC＝∠ACB，∠A＝50°，P是△ABC内一点，且∠ACP＝∠PBC，则∠BPC的度数为（ ）

    A. 130° B. 115° C. 110° D. 105°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家－“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.

    以为例，花拉子米的几何解法如下：

    如图，在边长为的正方形的两个相邻边上作边长分别为和5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形.

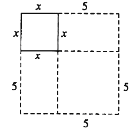
    通过不同的方式来表达大正方形的面积，可以将原方程化为 ）2=39+ ，从而得到此方程的正根是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠BAC=120°，DE垂直平分AC，交BC于D，交AC于E，且DE=2cm，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．

    解：设x2－4x=y

    原式=（y+2）（y+6）+4 （第一步）

    =y2+8y+16 （第二步）

    =（y+4）2（第三步）

    =（x2－4x+4）2（第四步）

    回答下列问题：

    （1）该同学第二步到第三步运用了因式分解的_______．

    A．提取公因式

    B．平方差公式

    C．两数和的完全平方公式

    D．两数差的完全平方公式

    （2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．

    （3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

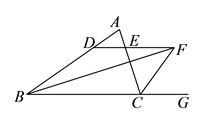
    【题目】如图，在中， ， 的平分线与的外角平分线交于点，过点作，交于点，交于点．

    （）图中除之外，还有几个等腰三角形，请分别写出来；

    （）若， ，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

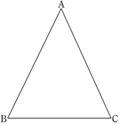
    【题目】如图所示，在△ABC中，∠ABC=∠ACB．

    （1）尺规作图：过顶点A，作△ABC的角平分线AD；(不写作法，保留作图痕迹)

    （2）在AD上任取一点E，连接BE、CE．求证：BE=CE．

    查看答案和解析>>

    同步练习册答案