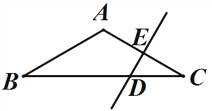
【题目】如图，在△ABC中，AB=AC，∠BAC=120°，DE垂直平分AC，交BC于D，交AC于E，且DE=2cm，求BC的长．
【答案】12cm
【解析】试题分析：首先连接AD，由DE垂直平分AC，根据线段垂直平分线的性质，易得AD=CD，又由在△ABC中，AB=AC，∠BAC=120°，易求得∠DAC=∠B=∠C=30°，继而可得∠BAD=90°，然后利用含30°角的直角三角形的性质，即可求得BC的长．
试题解析：连接AD，
∵DE垂直平分AC，
∴AD=CD，∠DEC=90°，
∴∠DAC=∠C，
∵在△ABC中，AB=AC，∠BAC=120°，
∴∠B=∠C=
=30°，
∴∠DAC=∠C=∠B=30°，
∴∠ADB=∠DAC+∠C=60°，
∴∠BAD=180°-∠B-∠ADB=90°，
在Rt△CDE中，∠C=30°，DE=2cm，
∴CD=2DE=4cm，
∴AD=CD=4cm，
在Rt△BAD中，∠B=30°，
∴BD=2AD=8cm，
∴BC=BD+CD=12（cm）．
寒假天地重庆出版社系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2－3x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x2－3x+m=0的两实数根是（ ）
A. x1=1，x2=－1 B. x1=1，x2=2 C. x1=1，x2=0 D. x1=1，x2=3
查看答案和解析>>
科目：初中数学 来源： 题型：
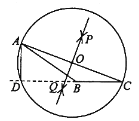
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知： 
.
求作： 
边上的高
作法：如图，
(1)分别以点
和点
为圆心，大于
的长为半径作弧，两弧相交于
， 
两点；
(2)作直线
，交
于点
；
(3)以
为圆心， 
为半径⊙O,与CB的延长线交于点D，连接AD，线段AD即为所作的高.
请回答；该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目：初中数学 来源： 题型：
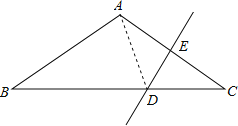
【题目】如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO=108°，则∠C的度数为（ ）
A. 40° B. 41° C. 32° D. 36°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC中，∠BAD=∠EBC，AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ；
(2)若∠ABC=35°，EG∥AD，EH⊥BE，求∠HEG的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学生在素质教育基地进行社会实践活动，帮助农民伯伯采摘了黄瓜和茄子共40kg，了解到这些蔬菜的种植成本共42元，还了解到如下信息：
（1）请问采摘的黄瓜和茄子各多少千克？
（2）这些采摘的黄瓜和茄子可赚多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
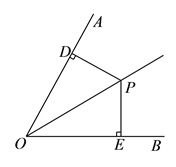
【题目】已知：如图， 
是
内一点， 
， 
， 
， 
分别是垂足，且
．
（
）求证：点
在
的平分线上．
（
）若点
是射线
上一点，点
是射线
上一点，且
， 
．
①当
是等腰三角形时，求点
到射线
的距离；
②连接
， 
， 
，当
的周长最小时，求
的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，在△ABC中，AB=AC，点P，D分别是BC，AC边上的点，且∠APD=∠B.
（1）求证:AC·CD=CP·BP;
（2）若AB=10，BC=12，当PD∥AB时，求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com