
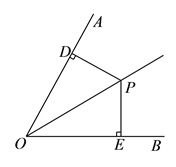
【题目】已知:如图, ![]() 是
是![]() 内一点,
内一点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是垂足,且
分别是垂足,且![]() .
.
(![]() )求证:点
)求证:点![]() 在
在![]() 的平分线上.
的平分线上.
(![]() )若点
)若点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() ,
, ![]() .
.
①当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 到射线
到射线![]() 的距离;
的距离;
②连接![]() ,
, ![]() ,
, ![]() ,当
,当![]() 的周长最小时,求
的周长最小时,求![]() 的度数.
的度数.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )①
)①![]() 或
或![]() 或
或![]() ;②
;②![]() .
.
【解析】试题分析:(1)证明![]() ≌
≌![]() ,根据全等三角形的对应角相等即可得;
,根据全等三角形的对应角相等即可得;
(2)①分![]() 或
或![]() 或
或![]() 三种情况进行讨论即可得;
三种情况进行讨论即可得;
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .作点
.作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
试题解析:(1)在![]() 和
和![]() 中,有
中,有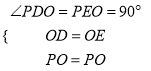 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 的平分线上;
的平分线上;
(2)①若![]() 是等腰三角形,则
是等腰三角形,则![]() 或
或![]() 或
或![]() .
.
(Ⅰ)若![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
∴![]() 到
到![]() 的距离为
的距离为![]() ;
;
(Ⅱ)若![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
∵![]() ,则
,则![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,设
,设![]() ,
,
则![]() ,
,
即![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ;
;
(Ⅲ)若![]() ,同理可知
,同理可知![]() .
.
综上,点![]() 到射线
到射线![]() 的距离为
的距离为![]() 或
或![]() 或
或![]() ;
;
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .
.
作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
如图所示:由轴对称性质可得,
OP1=OP2=OP,∠P1OA=∠POA,∠P2OB=∠POB,
所以∠P1OP2=2∠AOB=2×60°=120°,
所以∠OP1P2=∠OP2P1=(180°-120°)÷2=30°,
又因为∠FPO=∠OP1F=30°,∠GPO=∠OP2G=30°,
所以∠FPG=∠FPO+∠GPO=60°.



科目:初中数学 来源: 题型:
【题目】有质地均匀的A、B、C、D四张卡片,上面对应的图形分别是圆、正方形、正三角形、平行四边形,将这四张卡片放入不透明的盒子中摇匀,从中随机抽出一张(不放回),再随机抽出第二张.
(1)如果要求抽出的两张卡片上的图形,既有圆又有三角形,请你用列表或画树状图的方法,求出出现这种情况的概率;
(2)因为四张卡片上有两张上的图形,既是中心对称图形,又是轴对称图形,所以小明和小东约定做一个游戏,规则是:如果抽出的两个图形,既是中心对称图形又是轴对称图形,则小明赢;否则,小东赢.问这个游戏公平吗?为什么?如果不公平,请你设计一个公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒,已知米=1000000微米,则2.5微米=0.0000025米,用科学记数法可以表示为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
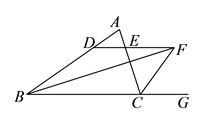
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的平分线
的平分线![]() 与
与![]() 的外角平分线交于点
的外角平分线交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(![]() )图中除
)图中除![]() 之外,还有几个等腰三角形,请分别写出来;
之外,还有几个等腰三角形,请分别写出来;
(![]() )若
)若![]() ,
, ![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(0,-1),B(0,3),C(-3,2).
(1) 描出A、B、C三点的位置,并画出三角形ABC;
(2) 三角形ABC中任意一点P(x,y)平移后的对应点为P1(x+3,y-2)将三角形ABC作同样的平移得到三角形A1B1C1,作出平移后的图形,并写出点A1、B1、C1的坐标;
(3) 求三角形A1B1C1的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com