
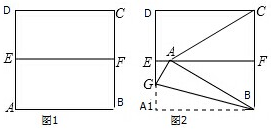
 如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理.
如何在一张正方形纸中折出一个等边三角形呢?如图①,对折正方形纸片ABCD,得到折痕EF,沿过点B的折痕将A角翻折,如图②使得点A落在EF上,连接AC,则△ABC即为等边三角形,请你说明这样做的道理. 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 22 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.
如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的一面靠墙(墙长22m),另外三面用90m长的铁栅栏围起来,如果这个存车处的面积为700m2,求这个长方形存车处的长和宽.查看答案和解析>>
科目:初中数学 来源: 题型:
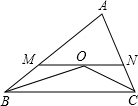 如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.
如图,O是△ABC中∠ABC平分线上的一点,过O作BC的平行线与AB、AC分别交于M、N两点,且有MN=BM+CN,连结CO.求证:CO平分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:
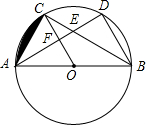 如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点;
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com