【题目】如图，已知∠ADC=90°，AD=8，CD=6，AB=26，BC=24．
（1）试说明：△ABC是直角三角形．
（2）请求图中阴影部分的面积．
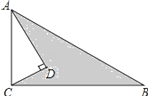
【答案】（1）证明见解析；（2）S阴影=96.
【解析】试题分析：（1）先根据勾股定理求出AC的长，再根据勾股定理的逆定理即可证明△ABC为直角三角形；（2）根据S阴影=SRt△ABC-SRt△ACD，利用三角形的面积公式计算即可求解．
试题解析：（1）∵在Rt△ADC中，∠ADC=90°，AD=8，CD=6，
∴AC2=AD2+CD2=82+62=100，
∴AC=10（取正值）．
在△ABC中，∵AC2+BC2=102+242=676，AB2=262=676，
∴AC2+BC2=AB2，
∴△ABC为直角三角形；
（2）S阴影=SRt△ABC﹣SRt△ACD
=
×10×24﹣
×8×6=96．
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案科目：初中数学 来源： 题型：
【题目】有一个几何体的形状为直三棱柱，右图是它的主视图和左视图．
(1)请补画出它的俯视图，并标出相关数据；
(2)根据图中所标的尺寸(单位：厘米)，计算这个几何体的全面积．
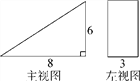
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共
亩，设种植娃娃菜
亩，总收益为
万元，有关数据见下表：
成本（单位：万元/亩） | 销售额（单位：万元/亩） | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
（1）求关于的函数关系式（收益 = 销售额 – 成本）；
（2）若计划投入的总成本不超过
万元，要使获得的总收益最大，基地应种植娃娃菜和油菜各多少亩？
（3）已知娃娃菜每亩地需要化肥
kg，油菜每亩地需要化肥
kg，根据（2）中的种植亩数，基地计划运送所需全部化肥，为了提高效率，实际每次运送化肥的总量是原计划的
倍，结果运送完全部化肥的次数比原计划少
次，求基地原计划每次运送多少化肥.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：矩形
，点
在
的延长线上，连接
，
，且
，
的平分线
交于点
．
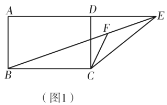
（1）如图1，求
的大小；
（2）如图2，过点作
交
的延长线于点
，求证：
；
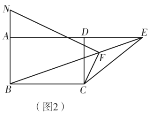
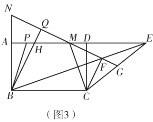
（3）如图3，在（2）的条件下，
交于点
，点
为
的中点，连接
交于点
，点
在
上，且
，连接
，且
．延长
交于点
，连接
，若
的周长与
的周长的差为2，求的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点D，E分别是不等边△ABC(即AB，BC，AC互不相等)的边AB，AC的中点．点O是△ABC所在平面上的动点，连接OB，OC，点G，F分别是OB，OC的中点，顺次连接点D，G，F，E.
(1)如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；
(2)若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？(直接写出答案，不需要说明理由)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在同一平面内，两条平行景观长廊l1和l2间有一条“U”形通道，其中AB段与景观长廊l1成45°角，长为20m；BC段与景观长廊垂直，长为10m，CD段与景观长廊l2成60°角，长为10m，求两景观长廊间的距离（结果保留根号）．
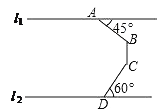
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知顶点为（﹣3，﹣6）的抛物线y=ax2+bx+c经过点（﹣1，﹣4），则下列结论中错误的是（ ）
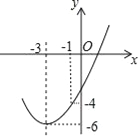
A. b2＞4ac
B. ax2+bx+c≥﹣6
C. 若点（﹣2，m），（﹣5，n）在抛物线上，则m＞n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
