
【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣1
(1)求抛物线的对称轴(用含m的式子去表示);
(2)若点(m﹣2,y1),(m,y2),(m+3,y3)都在抛物线y=x2﹣2mx+m2﹣1上,则y1、y2、y3的大小关系为 ;
(3)直线y=﹣x+b与x轴交于点A(3,0),与y轴交于点B,过点B作垂直于y轴的直线l与抛物线y=x2﹣2mx+m2﹣1有两个交点,在抛物线对称轴右侧的点记为P,当△OAP为钝角三角形时,求m的取值范围.
【答案】(1)x![]() m;(2)y2>y3>y1;(3)m<5.
m;(2)y2>y3>y1;(3)m<5.
【解析】
(1)函数的对称轴为:x![]() m;
m;
(2)函数对称轴为x=m,函数开口向上,x=m时函数取得最小值,即可求解;
(3)分∠OPA是钝角、∠OAP是钝角两种情况,分别求解即可.
解:(1)函数的对称轴为:x![]() m;
m;
(2)函数对称轴为x=m,函数开口向上,x=m时函数取得最小值,
故:y2>y3>y1;
(3)把点A的坐标代入y=﹣x+b的表达式并解得:b=3,
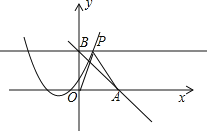
则点B(0,3),直线表达式为:y=﹣x+3,
当y=3时,y=x2﹣2mx+m2﹣1=3,
则x=m±2,则点P(m﹣2,3),
则OP2=(m﹣2)2+9,OA2=9,PA2=(m﹣5)2+9,
①当∠OPA是钝角时,
则OP2+PA2>OA2,
即:(m﹣2)2+9+(m﹣5)2+9>9,
解得:m为任意实数;
②当∠OAP是钝角时,
OA2+PA2>OP2,
即9+(m﹣5)2+9>(m﹣2)2+9
解得:m<5.
即:m的取值范围为:m<5.


科目:初中数学 来源: 题型:
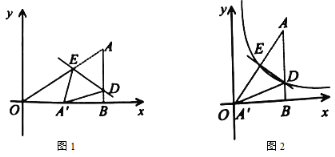
【题目】如图1,点A在第一象限,![]() 轴于B点,连结
轴于B点,连结![]() ,将
,将![]() 折叠,使
折叠,使![]() 点落在x轴上,折痕交
点落在x轴上,折痕交![]() 边于D点,交斜边
边于D点,交斜边![]() 于E点,(1)若A点的坐标为
于E点,(1)若A点的坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标是______;(2)若
的坐标是______;(2)若![]() 与原点O重合,
与原点O重合,![]() ,双曲线
,双曲线![]() 的图象恰好经过D,E两点(如图2),则
的图象恰好经过D,E两点(如图2),则![]() ____.
____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
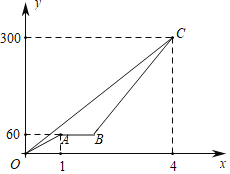
【题目】甲车与乙车同时从A地出发去往B地,如图所示,折线O﹣A﹣B﹣C和射线OC分别是甲、乙两车行进过程中路程与时间的关系,已知甲车中途有事停留36分钟后再继续前往C地,两车同时到达C地,则下列说法:①乙车的速度为70千米/时;②甲车再次出发后的速度为100千米/时;③两车在到达B地前不会相遇;④甲车再次出发时,两车相距60千米.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
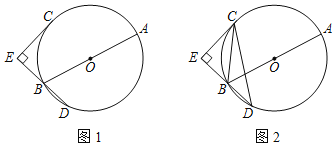
【题目】已知:AB为⊙O的直径,C、D为心⊙O上的点,C是优弧AD的中点,CE⊥DB交DB的延长线于点E.
(1)如图1,判断直线CE与⊙O的位置关系,并说明理由.
(2)如图2,若tan∠BCE=![]() ,连BC、CD,求cos∠BCD的值.
,连BC、CD,求cos∠BCD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com