
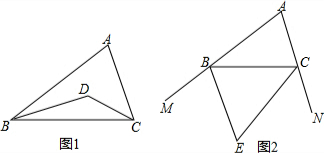
 (1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.分析 (1)①根据角平分线的定义得到∠ABD=∠CBD,∠BCD=∠ACD,再根据三角形内角和定理得到∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,利用等量代换得到2(180°-∠BDC)+∠A=180°,即有∠BDC=90°+$\frac{1}{2}$∠A;
②利用①直接表示即可;
(2)先根据BE、CE分别是∠CBM、∠BCN的平分线可知∠EBC=$\frac{1}{2}$∠MBC,∠BCE=$\frac{1}{2}$∠BCM,再由∠CBM、∠BCN是△ABC的两个外角得出∠CBM+∠BCN=360°-(180°-∠A)=180°+∠A,故∠EBC+∠BCE=$\frac{1}{2}$(∠MBC+∠BCN)=$\frac{1}{2}$(180°+∠A)=90°+$\frac{1}{2}$∠A,根据在△EBC中∠BEC=180°-(∠EBC+∠BCE)即可得出结论.
解答 解:(1)①∵∠ABC,∠ACB的平分线相交于点D,
∴∠ABD=∠CBD,∠BCD=∠ACD,
∵∠DBC+∠BCD+∠BDC=180°,∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°,
∴2∠DBC+2∠BCD+∠A=180°,
∴2(180°-∠BDC)+∠A=180°,
∴∠BDC=90°+$\frac{1}{2}$∠A,
∵∠A=70°,
∴∠BDC=90°+$\frac{1}{2}$×70°=90°+35°=125°.
②∠A=90°+$\frac{1}{2}$α.
(2)∵BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线,
∴∠EBC=$\frac{1}{2}$∠MBC,∠BCE=$\frac{1}{2}$∠BCM,
∵∠CBM、∠BCN是△ABC的两个外角
∴∠CBM+∠BCN=360°-(180°-∠A)=180°+∠A
∴∠EBC+∠BCE=$\frac{1}{2}$(∠MBC+∠BCN)=$\frac{1}{2}$(180°+∠A)=90°+$\frac{1}{2}$∠A,
在△DBC中,
∵∠BEC=180°-(∠EBC+∠BCE)
=180°-(90°+$\frac{1}{2}$∠A)
=90°-$\frac{1}{2}$∠A,且∠A=α,
∴∠BEC=90°-$\frac{1}{2}$α.
点评 本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ | B. | -22与(-2)2 | C. | -(-1)2011与(-1)2010 | D. | (-5)2与-52 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
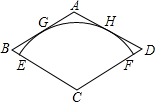 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
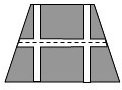 如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?
如图,要设计一个等腰梯形的花坛,花坛上底长120m,下底长180m,上下底相距80m,在两腰中点连线外有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等,甬道的面积是梯形面积的八分之一.甬道的宽应是多少(精确到0.01m)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
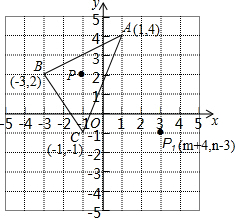 如图,三角形ABC中任一点P(m,n)经平移后对应点为P1(m+4,n-3),将三角形ABC作同样的平移得到三角形A1B1C1.
如图,三角形ABC中任一点P(m,n)经平移后对应点为P1(m+4,n-3),将三角形ABC作同样的平移得到三角形A1B1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com