
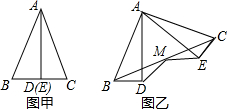
 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME. 分析 利用等腰三角形的性质以及选择的性质可证明△MBD≌△MCE,由全等三角形的性质即可证明MD=ME.
解答 证明:
∵将△ABD绕点A逆时针旋转到△AEC,(如图乙)
∴AB=AC,BD=CE,
∴∠ABC=∠ACB,
∵AB=AC,(如图甲)
∴∠ABD=∠ACD,
∴∠DBM=∠ECM,
∵M是BC中点,
∴BM=CM,
在△MBD和△MCE中
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$,
∴△MBD≌△MCE(SAS),
∴MD=ME.
点评 本题考查了旋转的性质、等腰三角形的性质以及全等三角形的判断和性质,熟记全等三角形的各种判断方法和性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
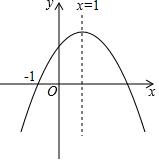 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com