
【题目】如图,已知等边三角形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别为各边中点,
分别为各边中点,![]() 为直线
为直线![]() 上一动点,
上一动点,![]() 为等边三角形(点
为等边三角形(点![]() 的位置改变时,
的位置改变时,![]() 也随之整体移动).
也随之整体移动).

(1)如图1,当点![]() 在点
在点![]() 左侧时,请判断
左侧时,请判断![]() 与
与![]() 有怎样的数量关系?请直接写出结论,不必证明或说明理由;
有怎样的数量关系?请直接写出结论,不必证明或说明理由;
(2)如图2,当点![]() 在
在![]() 上时,其它条件不变,(1)的结论中
上时,其它条件不变,(1)的结论中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)若点![]() 在点
在点![]() 右侧时,请你在图3中画出相应的图形,并判断(1)的结论中
右侧时,请你在图3中画出相应的图形,并判断(1)的结论中![]() 与
与![]() 的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接
的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.(提示:连接![]() 、
、![]() 、
、![]() .可证
.可证![]() 、
、![]() 、
、![]() 、
、![]() 均为等边三角形).
均为等边三角形).
【答案】(1)![]() ,(2)成立证明见解析;(3)结论仍成立.
,(2)成立证明见解析;(3)结论仍成立.
【解析】
(1)连接DE,DF,得出△DFE是等边三角形,那么∠DEF=∠DFM=60°,DE=DF,再利用SAS证明△MDF和△EDN全等,由此可得出EN=MF.
(2)(3)证法同(1)都要证明△MDF和△EDN全等,证明过程中都要作出三角形的三条中位线,然后根据三条中位线分成的小等边三角形的边和角相等来得出两三角形全等的条件,因此结论仍然成立.
解:(1)EN=MF.理由如下:连接DE,DF,
∵△ABC是等边三角形,∴AB=AC=BC.
又∵D,E,F是三边的中点,∴EF=DF=BF.
∴∠DEF=∠DFM=60°,
又△MDN为等边三角形,∴∠MDN=60°,
∠MDN+∠NDF=∠FDE+∠NDF,
∴∠MDF=∠NDE,
在△EDN和△MDF中,

∴△EDN≌△MDF(SAS),
∴EN=MF.
(2)如图②,EN=MF仍然成立.证明如下:连接DF,NF, 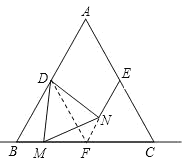
∵△ABC是等边三角形,∴AB=AC=BC.
又∵D,E,F是三边的中点,∴EF=DF=BF.
∵∠BDM+∠MDF=60°,∠FDN+∠MDF=60°,
∴∠BDM=∠FDN,
在△DBM和△DFN中,

∴△DBM≌△DFN,
∴BM=FN,∠DFN=∠FDB=60°,
∴NF∥BD,
∵E,F分别为边AC,BC的中点,
∴EF是△ABC的中位线,
∴EF∥BD,
∴F在直线NE上,
∵BF=EF,
∴MF=EN.
(3)如图③,MF=NE的结论仍然成立.
连接DF、DE,
由(2)知DE=DF,∠NDE=∠FDM,DN=DM,
在△DNE和△DMF中,

∴△DNE≌△DMF,
∴MF=NE.


科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 是两块可以完全重合的三角板,
是两块可以完全重合的三角板,![]() ,
,![]() . 在图1所示的状态下,
. 在图1所示的状态下,![]() 固定不动,将
固定不动,将![]() 沿直线
沿直线![]() 向左平移.
向左平移.
(1)当![]() 移到图2位置时连接位綱连接
移到图2位置时连接位綱连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
(2)如图3,在上述平移过程中,当点![]() 与
与![]() 的中点重合时,直线
的中点重合时,直线![]() 与AD有什么位置关系,请写出证明过程.
与AD有什么位置关系,请写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x(元) | 3000 | 3200 | 3500 | 4000 |
y(辆) | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数(辆) | ________ | 未租出的车辆数(辆) | ________ |
租出每辆车的月收益(元) | ________ | 所有未租出的车辆每月的维护费(元) | ________ |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
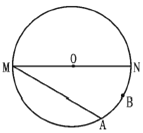
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点.
的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,小刚同学按如下步骤作图:
(1)以B为圆心,BC长为半径画弧,交AB于点E
(2)分别以点C.E为圆心,大于![]() CE的长为半径画弧,两弧在△ABC内相交于点P
CE的长为半径画弧,两弧在△ABC内相交于点P
(3)连接BP,并延长交AC于点D
(4)连接DE
根据以上作图步骤,有下列结论:①BD平分∠ABC; ②AD+DE = AC;③点P与点D关于直线CE对称; ④△BCD与△BED关于直线BD对称.
其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了甲、乙两种新品饮料,它们都由A、B、C三种溶液组成,只是甲种饮料每瓶装有200克A溶液,200克B溶液,100克C溶液;乙种饮料每瓶装有100克A溶液,100克B溶液,300克C溶液,甲、乙两种饮料每瓶成本价均为瓶中A、B、C三种溶液的成本价之和.已知C种溶液每一百克的成本价为1元,乙种饮料每瓶售价为10元,利润率为![]() ,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com