
已知:如图,点 在线段
在线段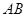 上,
上, 是等边三角形.(1)当
是等边三角形.(1)当 满足怎样的关系式时
满足怎样的关系式时 ;(2)当
;(2)当 时,求
时,求 的度数.
的度数.
(1)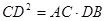 ;(2)
;(2)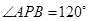
【解析】
试题分析:(1)先根据等边三角形的性质可得PC=CD=PD,∠PCD=∠PDC=60°,即可得到∠PCA=∠PDB=120°,再有 ,即可证得结果.
,即可证得结果.
(2)由 可得∠A=∠DPB,再结合等边三角形的性质即可求得结果.
可得∠A=∠DPB,再结合等边三角形的性质即可求得结果.
(1)∵ 是等边三角形
是等边三角形
∴PC=CD=PD,∠PCD=∠PDC=∠CPD=60°
∴∠PCA=∠PDB=120°
∵ ,即
,即 ,
,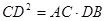
∴ ;
;
(2)∵ 时,
时,
∴∠A=∠DPB
∵∠PCD=∠A+∠APC=60°
∴∠DPB+∠APC=60°
∵∠CPD=60°
∴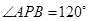 .
.
考点:等边三角形的性质,相似三角形的判定和性质
点评:等边三角形的判定和性质的应用是初中数学的重点和难点,与各个知识点的结合极为容易,因而是中考的热点,尤其在压轴题中极为常见,一般难度不大,需熟练掌握.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| ||
| 6 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
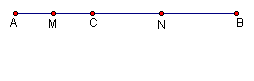
已知,如图,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.(1)求线段
的中点.(1)求线段![]() 的长度;
的长度;
(2)在(1)中,如果![]() ,
,![]() ,其它条件不变,你能猜测出
,其它条件不变,你能猜测出![]() 的长度吗?请说出你发现的结论,并说明理由.
的长度吗?请说出你发现的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,点![]() 为线段
为线段![]() 上一点,
上一点,![]() 、
、![]() 是等边三角形,可以说明:
是等边三角形,可以说明:![]() ≌
≌![]() ,从而得到结论:
,从而得到结论:![]() .现要求:
.现要求:
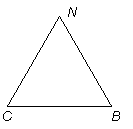
(1)将![]() 绕
绕![]() 点按逆时针方向旋转180°,使
点按逆时针方向旋转180°,使![]() 点落在
点落在![]() 上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).
(2)在(1)所得到的图形中,结论“![]() ”是否还成立?若成立,请给予证明;若不成立,请说明理由.
”是否还成立?若成立,请给予证明;若不成立,请说明理由.
(3)在(1)所得到的图形中,设![]() 的延长线与
的延长线与![]() 相交于
相交于![]() 点,请你判断△ABD与四边形
点,请你判断△ABD与四边形![]() 的形状,并说明你的结论的正确性.
的形状,并说明你的结论的正确性.
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com