
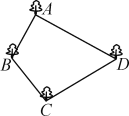
【题目】张大伯承包了一个四边形的池塘,如图所示,它的四个角A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图.
【答案】见解析
【解析】
此题的关键是读懂题意,即理解张大伯的意思,把地扩大成平行四边形,而且面积要为原来的一倍.就可连接对角线AC,BD交于点O,过点A作BD的平行线,过点C作BD的平行线,过点B作AC的平行线,过点D作AC的平行线,四条平行线依次交于M,N,G,H四点,则可得四边形AODH,AOBM,BOCN,OCGD均为平行四边形.由全等形就可证明扩大后的是原来的一倍.
如图所示.
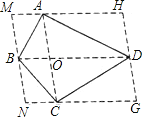
连接对角线AC,BD交于点O,
过点A作BD的平行线,过点C作BD的平行线,
过点B作AC的平行线,过点D作AC的平行线,
四条平行线依次交于M,N,G,H四点,
则可得四边形AODH,AOBM,BOCN,OCGD均为平行四边形.
在AODH中,AO=HD,AH=OD,AD=AD,
∴△AHD≌△AOD.
∴S△AHD=S△AOD,同理S△COD=S△CGD,S△ABM=S△ABO,S△BCO=S△BCN.
∴SMNGH=2S四边形ABCD,MNGH即为所示.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
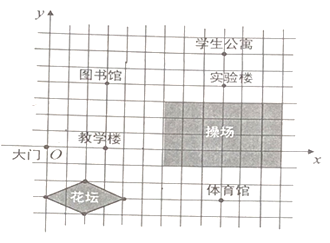
【题目】(1)如图,是某学校的平面简图,以学校大门位置为坐标原点建立平面直角坐标系.写出图中教学楼、图书馆、体育馆、实验楼、学生公寓位置的坐标(网格小正方形的边长记为1个长度单位).
教学楼:_____________;
图书馆:_____________;
体育馆:_____________;
实验楼:_____________;
学生公寓:_____________;
(2)点![]() 在坐标系中的位置如图所示,三角形
在坐标系中的位置如图所示,三角形![]() 的面积为
的面积为![]()
①三角形![]() 三个顶点的坐标分别为:
三个顶点的坐标分别为:![]() (____,____),
(____,____),![]() (____,_____),
(____,_____),![]() (__,__);
(__,__);
②点![]() 是一动点,若三角形
是一动点,若三角形![]() 面积等于三角形
面积等于三角形![]() 面积.求点
面积.求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
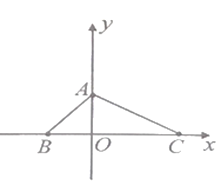
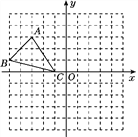
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
(2)作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
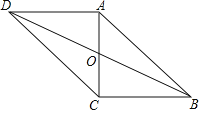
【题目】如图,在ABCD中,对角线AC、BD交于点O,AC⊥BC,且ABCD的周长为36,△OCD的周长比△OBC的周长大2.
(1)求BC,CD的长;
(2)求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标分别是点
的坐标分别是点![]() ,
,![]() ,且
,且![]() 满足:
满足:![]() .
.
(1)则![]() _________,
_________,![]() _________;
_________;
(2)![]() 为
为![]() 轴负半轴上一点,过点
轴负半轴上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
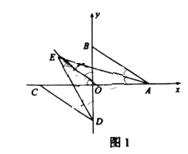
①如图1,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
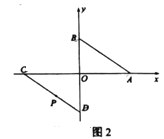
②如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
A. AB=CD
B. AC=BD
C. ∠A=∠D
D. ∠A=∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8中图①,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向
右平移到△A′B′D′的位置得到图②,则阴影部分的周长为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需要将方向调整到与出发时一致,则方向的调整应为( )

A.左转80°B.右转80°C.左转100°D.右转100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com