
【题目】如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.
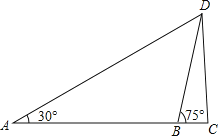
(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
【答案】(1)20m;(2)塔高CD为(10+10![]() )m.
)m.
【解析】
试题分析:(1)过点B作BE⊥AD于点E,然后根据AB=40m,∠A=30°,可求得点B到AD的距离;
(2)先求出∠EBD的度数,然后求出AD的长度,然后根据∠A=30°即可求出CD的高度.
解:(1)过点B作BE⊥AD于点E,
∵AB=40m,∠A=30°,
∴BE=![]() AB=20m,AE=
AB=20m,AE=![]() =20
=20![]() m,
m,
即点B到AD的距离为20m;
(2)在Rt△ABE中,
∵∠A=30°,
∴∠ABE=60°,
∵∠DBC=75°,
∴∠EBD=180°﹣60°﹣75°=45°,
∴DE=EB=20m,
则AD=AE+EB=20![]() +20=20(
+20=20(![]() +1)(m),
+1)(m),
在Rt△ADC中,∠A=30°,
∴DC=![]() =(10+10
=(10+10![]() )m.
)m.
答:塔高CD为(10+10![]() )m.
)m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某课题组为了解全市八年级学生对数学知识的掌握情况,在一次数学检测中,从全市24000名八年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:

请根据以上图表提供的信息,解答下列问题:
(1)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() = ,
= ,![]() = ;
= ;
(2)请在图中,补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市24000名八年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
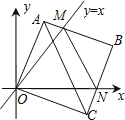
【题目】在平面直角坐标系中,边长为3的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).在旋转正方形OABC的过程中,△MBN的周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com