
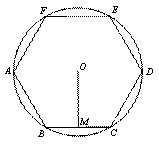
如图,正六边形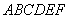 内接于圆
内接于圆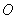 ,半径为
,半径为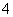 ,则这个正六边形的边心距
,则这个正六边形的边心距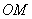 和
和
弧 的长分别为
的长分别为
(A) 、
、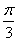 (B)
(B)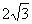 、
、
(C)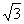 、
、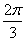 (D)
(D)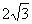 、
、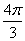
科目:初中数学 来源: 题型:
设函数y=(x−1)[(k−1)x+(k−3)]( k是常数)
k是常数)
1) 当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象
2) 根据图象,写出你发现的一条结论[来源:学.科.网]
3) 将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
已知一个函数图像经过(1. -4) (2. -2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是
A. 正比例函数 B. 一次函数 c. 反比例函数 D.二次函数
查看答案和解析>>
科目:初中数学 来源: 题型:
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”。
(1)概念理解
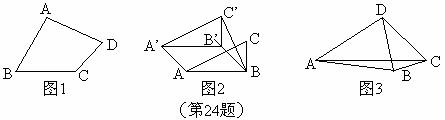
如图1,在四边形ABCD中,添加一个条件,使得四边形ABCD是“等邻边四边形”,请写出你添加的一个条件;2-1-c-n-j-y
(2)问题探究
①小红猜想:对角线互相平分的“等邻边四边形”是菱形,她的猜想正确吗?请说明理由;
②如图2,小红画了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将Rt△ABC沿∠B的平分线BB’方向平移得到△A’B’C’,连结AA’,BC’。小红要使平移后的四边形ABC’A’是“等邻边四边形”,应平移多少距离(即线段BB’的长)?
(3)应用拓展
如图3,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,AC=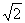 AB。试探究BC,CD,BD的数量关系。
AB。试探究BC,CD,BD的数量关系。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com