
 已知,如图1,点A、B分别在x轴、y轴正半轴上,∠OAB、∠OBA的平分线相交于点E,分别交x轴、y轴于点D、C.
已知,如图1,点A、B分别在x轴、y轴正半轴上,∠OAB、∠OBA的平分线相交于点E,分别交x轴、y轴于点D、C.分析 (1)根据角平分线的定义以及三角形内角和定理,即可求得∠AEB的度数;
(2)先连接OE,根据点E是△ABO的内心,以及C、O、Q、E四点共圆,求得∠EOQ=∠ECQ=45°,再根据∠CED=∠AEB=135°,得出∠ECQ+∠CED=180°,进而判定CQ∥BD,得出∠PCQ=∠OBD,最后得到∠PCQ=$\frac{1}{2}$∠ABO.
解答 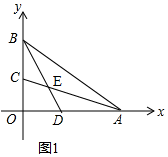 解:(1)如图1,∵∠AOB=90°,
解:(1)如图1,∵∠AOB=90°,
∴∠ABO+∠BAO=90°,
∵∠OAB、∠OBA的平分线相交于点E,
∴∠EBA+∠EAB=$\frac{1}{2}$∠ABO+$\frac{1}{2}$∠BAO=$\frac{1}{2}$(∠ABO+∠BAO)=$\frac{1}{2}$×90°=45°,
∴△ABE中,∠AEB=180°-45°=135°;
(2)如图2,连接OE,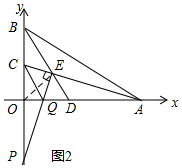 则根据点E是△ABO的内心可得,OE平分∠AOB,
则根据点E是△ABO的内心可得,OE平分∠AOB,
∴∠EOA=45°,
∵PE⊥AC于E,∠COQ=90°,
∴C、O、Q、E四点共圆,
∴∠EOQ=∠ECQ=45°,
∵∠CED=∠AEB=135°,
∴∠ECQ+∠CED=180°,
∴CQ∥BD,
∴∠PCQ=∠OBD,
又∵∠OBD=$\frac{1}{2}$∠ABO,
∴∠PCQ=$\frac{1}{2}$∠ABO.
点评 本题主要考查了三角形内角和定理以及平行线的判定,解决问题的关键是运用四点共圆进行求解.解题时注意:三角形的内心与三角形顶点的连线平分这个内角;将四点连成一个四边形,若对角互补,那么这四点共圆.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
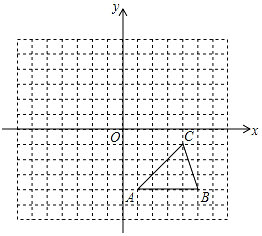 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出数量(件) | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价(元) | +3 | +2 | +1 | 0 | -1 | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com