Question

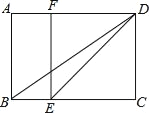
【题目】已知：如图，在矩形ABCD中，E是BC边一点，DE平分∠ADC，EF∥DC角AD边于点F，连结BD．

（1）求证：四边形EFCD是正方形；

（2）若BE=1，ED=2，求BD的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）先证明四边形FECD为平行四边形，再证出CD＝CE，得出四边形FECD为菱形，由∠C＝90°，即可得出四边形FECD为正方形；

（2）先由三角函数求出正方形FECD的边长CD＝CE，得出BC，进而得出BD的长．

（1）∵四边形ABCD是矩形，

∴AD∥BC，∠ADC=∠C=90°，

∵EF∥DC，

∴四边形FECD为平行四边形，

∵DE平分∠ADC，

∴∠ADE=∠CDE，

∵AD∥BC，

∴∠ADE=∠DEC，

∴∠CDE=∠DEC，

∴CD=CE，

∴四边形FECD是菱形，

又∵∠C=90°，

∴平行四边形FECD是正方形；

（2）∵四边形FECD是正方形，

∴∠CDE=45°，

∵ED=2，

∴CE=CD=EDsin45°=2×=2，

∴BC=BE+EC=1+2=3，

∴BD2=BC2+CD2=32+22=13，

∴BD=．