
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

【答案】DE=BF,DE⊥BF.理由见解析.
【解析】试题分析:本题首先要给出答案,在说明理由. 连接DB,根据DH是AB的垂直平分线得出∠A=∠DBH,再根据三角形外角的性质得出∠CDB=∠A+∠DBH,故可得出CD=CB.由SAS定理得出△ECD≌△FCB,所以ED=FB,∠DEC=∠BFC,∠DEC+∠FBC=90°,进而可得出结论.
试题解析:
DE=BF,DE⊥BF.
理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
又∵CE=CF,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.



科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣6,0)、B(﹣2,3)、
C(﹣1,0).
(1)请直接写出与点B关于坐标原点O的对称点B1的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形,直接写出点A的对应点A′的坐标;
(3)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是_____度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_____等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD.有下列四个结论:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直线MB垂直平分线段CD;(4)四边形ABCD是轴对称图形.其中正确结论的个数为( )
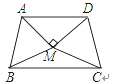
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 
A.①②
B.②③
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)计算:
(1)3·(x4)6-2(x5·x3)3+x11·x13+x20·x3·x;
(2)(-4×103)2×(-2×103)2;
(3) ![]() 100×
100×![]() 99×
99×![]() 100;
100;
(4) ![]() 2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
2 015·(x2)2 015-(-0.125)3×29+(-0.25)2 014×42 014;
(5)162m÷42n÷4m×43m-3n+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )

A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com