
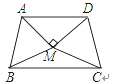
【题目】如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD.有下列四个结论:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直线MB垂直平分线段CD;(4)四边形ABCD是轴对称图形.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】(1)∵△ABM≌△CDM,△ABM、△CDM都是等边三角形,
∴∠ABM=∠AMB=∠BAM=∠CMD=∠CDM=∠DCM=60°,AB=BM=AM=CD=CM=DM,
又∵MA⊥MD,
∴∠AMD=90°,
∴∠BMC=360°60°6090°=150°,
又∵BM=CM,
∴∠MBC=∠MCB=15°;
(2)∵AM⊥DM,
∴∠AMD=90°,
又∵AM=DM,
∴∠MDA=∠MAD=45°,
∴∠ADC=45°+60°=105°,
∠ABC=60°+15°=75°,
∴∠ADC+∠ABC=180°;
(3)延长BM交CD于N,
∵∠NMC是△MBC的外角,
∴∠NMC=15°+15°=30°,
∴BM所在的直线是△CDM的角平分线,
又∵CM=DM,
∴BM所在的直线垂直平分CD;
(4)根据(2)同理可求∠DAB=105°,∠BCD=75°,
∴∠DAB+∠ABC=180°,
∴AD∥BC,
又∵AB=CD,
∴四边形ABCD是等腰梯形,
∴四边形ABCD是轴对称图形。
故(2)(3)(4)正确。
故选C.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=(x﹣1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),点D与点C关于抛物线的对称轴对称.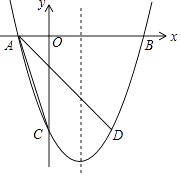
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程2x2﹣2x+1﹣3m=0的两个实数根,且x1、x2满足不等式x1x2+2(x1+x2)>0,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com