
【题目】(1)(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
如图①,在△ABC中,AD是△ABC的中线,若AB=10,AC=8,求AD的取值范围.
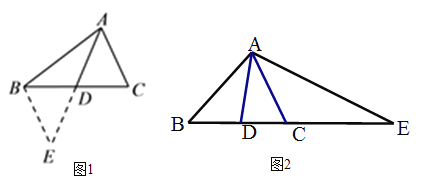
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是________.
A.SSS B.SAS C.AAS D.ASA
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是________.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)(学会运用)
如图②,AD是 △ABC的中线,点E在BC的延长线上,CE=AB, ∠BAC=∠BCA, 求证:AE=2AD.
【答案】(1)Ⅰ.B;Ⅱ. 1<AD<9;(2)证明见解析.
【解析】
(1)Ⅰ.根据全等三角形的判定定理解答;
Ⅱ.根据三角形的三边关系定理可得ABBE<AE<AB+BE,结合BE=AC可确定AE的取值范围,易得AD的取值范围;
(2)首先延长AD至M,使DM=AD,先证明△ABD≌△MCD,进而得出MC=AB,∠B=∠MCD,即可得出∠ACM=∠ACE,再证明△ACM≌△ACE,即可证明结论.
解:(1)Ⅰ.在△ADC和△EDB中,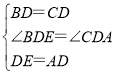 ,
,
∴△ADC≌△EDB(SAS),
故选:B;
Ⅱ.∵△ADC≌△EDB,
∴BE=AC,
∵ABBE<AE<AB+BE,
∴AB AC<AE<AB+AC,即2<AE<18,
∴1<AD<9,
故答案为:1<AD<9;
(2)延长AD至M,使DM=AD,
∵AD是△ABC的中线,
∴BD=CD,
在△ABD和△MCD中,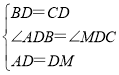 ,
,
∴△ABD≌△MCD(SAS),
∴MC=AB,∠B=∠MCD,
∵AB=CE,
∴CM=CE,
∵∠BAC=∠BCA,
∴∠B+∠BAC=∠ACB+∠MCD,即∠ACE=∠ACM,
在△ACE和△ACM中,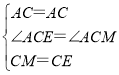 ,
,
∴△ACM≌△ACE(SAS),
∴AE=AM,
∵AM=2AD,
∴AE=2AD.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )


A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
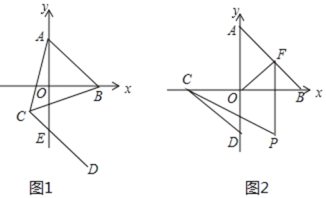
【题目】.如图 1,在平面直角坐标系中,A 、B 在坐标轴上,其中 A(0, a) ,B(b, 0)满足| a 3 |![]() 0.
0.
(1)求 A 、 B 两点的坐标;
(2)将 AB 平移到CD , A 点对应点C(2, m) , DE 交 y 轴于 E ,若ABC 的面积等于13,求点 E 的坐标;
(3)如图 2,若将 AB 平移到CD ,点 C、D 也在坐标轴上,F 为线段 AB 上一动点,(不包括点 A ,点B) ,连接OF 、FP 平分BFO ,BCP 2PCD,试探究COF,OFP ,CPF 的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
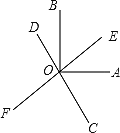
【题目】如图,直线EF、CD相交于点O,OA⊥OB,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
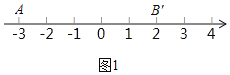
【题目】(1)对数轴上的点P进行如下操作:先把点P表示的数乘以![]() ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是 ,若点B′表示的数是2,则点B表示的数是 ;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是 .
,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴t,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是 ,若点B′表示的数是2,则点B表示的数是 ;已知线段AB上的点E经过上述操作后得到的对应点E'点E重合,则点E表示的数是 .
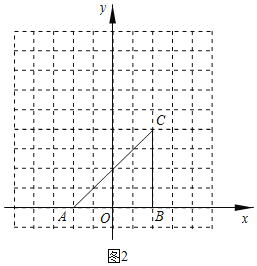
(2)在平面直角坐标系xOy中,已知△ABC的顶点A(﹣2,0),B(2,0),C(2,4),对△ABC及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同个实数a,将得到的点先向右平移m单位,冉向上平移n个单位(m>0,n>0),得到△ABC及其内部的点,其中点A,B的对应点分别为A′(1,2),B′(3,2).△ABC内部是否存在点F,使得点F经过上述操作后得到的对应点F′与点F重合,若存在,求出点F的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】粮库3天内发生粮食进出库的吨数如下(+表示进库-表示出库)+26,-32,-15,+34,-38,-20
(1)经过这3天,库里的粮食是增多还是减少了?
(2)经过这3天,仓库管理员结算发现库里还存480吨粮,那么3天前库里存粮多少吨?
(3)如果进出的装御费都是每吨5元,那么这3天要付多少装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kPa)是气体体积V(m3)的反比例函数,其图像如图所示.当气球内的气压大于150 kPa时,气球将爆炸.为了安全起见,气体的体积应不小于________m3.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com