
【题目】大家知道|1|=|1-0|,它的几何意义是,在数轴上表示数1的点与原点(即表示0的点)之间的距离.又如式子|4-2|,它在数轴上的意义是表示数4的点和表示数2的点之间的距离.
类似地,(1)写出式子|a-5|在数轴上的意义是,
(2)写出式子|b+4|在数轴上的意义是,
(3)若|x+2|=3,则x=.
(4)若|x-1|+|x-2|=3,则x为_________.
【答案】(1)在数轴上表示数a的点与表示数5的点之间的距离.(2)在数轴上表示数b的点与表示数-4的点之间的距离.(3)1或-5,(4)0或3.
【解析】
(1)根据绝对值的几何意义回答即可.(2)根据绝对值的几何意义回答即可.(3)根据绝对值的定义计算即可.(4)根据x的取值范围分类讨论计算即可.
(1)根据绝对值的几何意义可知∣a-5∣在数轴上的意义是:在数轴上表示数a的点与表示数5的点之间的距离.
(2)根据绝对值的几何意义可知∣b+4∣在数轴上的意义是:在数轴上表示数b的点与表示数-4的点之间的距离.
(3)∵∣x+2∣=3,
∴x+2=![]() 3,
3,
∴x=1,或x=-5,
(4)①当x<1时:|x-1|+|x-2|=1-x+2-x=3,x=0,
②当1≤x<2时:|x-1|+|x-2|=x-1+2-x=3,方程无解,
③当x≥2时:|x-1|+|x-2|=x-1+x-2=3,x=3,
故答案为:(1)在数轴上表示数a的点与表示数5的点之间的距离.(2)在数轴上表示数b的点与表示数-4的点之间的距离.(3)1或-5,(4)0或3.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B. 
(1)请你在图中把图补画完整;
(2)求C′B的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有颜色不同的黄、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复![]()
![]() 下表是活动中的一组统计数据:
下表是活动中的一组统计数据:

(1)请估计:当n很大时,摸到白球的频率将会接近______;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请你设计一个增(减)袋中白球或黄球球个数的方案,使得从袋中摸出一个球,这只球是黄球的概率大于是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线![]() 相交于点
相交于点![]() 于点
于点![]() 于点F,连结
于点F,连结![]() ,则下列结论:
,则下列结论:![]() ;
;![]() ;
;![]() ;
;![]() 图中共有四对全等三角形
图中共有四对全等三角形![]() 其中正确结论的个数是
其中正确结论的个数是![]()

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
![]() 设每件童装降价x元时,每天可销售______件,每件盈利______元;
设每件童装降价x元时,每天可销售______件,每件盈利______元;![]() 用x的代数式表示
用x的代数式表示![]()
![]() 每件童装降价多少元时,平均每天赢利1200元.
每件童装降价多少元时,平均每天赢利1200元.
![]() 要想平均每天赢利2000元,可能吗?请说明理由.
要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连结四边形各边中点所得的四边形是矩形,则原四边形( )
A. 一定是矩形 B. 一定是菱形 C. 对角线一定相等 D. 对角线一定互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC. 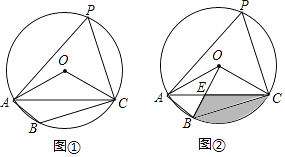
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ![]() ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.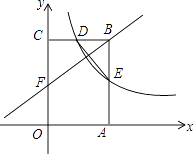
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com