
【题目】诸暨某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“五一”国际劳动节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
![]() 设每件童装降价x元时,每天可销售______件,每件盈利______元;
设每件童装降价x元时,每天可销售______件,每件盈利______元;![]() 用x的代数式表示
用x的代数式表示![]()
![]() 每件童装降价多少元时,平均每天赢利1200元.
每件童装降价多少元时,平均每天赢利1200元.
![]() 要想平均每天赢利2000元,可能吗?请说明理由.
要想平均每天赢利2000元,可能吗?请说明理由.
科目:初中数学 来源: 题型:
【题目】如图1所示,在正方形ABCD中,AB=1, ![]() 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作 ![]() 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点. 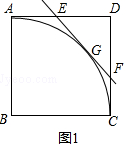
(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1 , D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由. 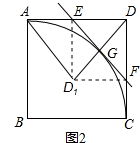
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣(﹣7)﹣(﹣5)+(﹣4)
(2)(﹣3![]() )+12.5+(﹣16
)+12.5+(﹣16![]() )﹣(﹣2.5)
)﹣(﹣2.5)
(3)(﹣24)×(![]() )
)
(4)18×(﹣![]() )+13×
)+13×![]() ﹣4×
﹣4×![]()
(5)﹣12018 - ![]() ×[2×(﹣2)+10].
×[2×(﹣2)+10].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E. 
(1)求证:DE是⊙O的切线;
(2)当AB=4 ![]() ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道|1|=|1-0|,它的几何意义是,在数轴上表示数1的点与原点(即表示0的点)之间的距离.又如式子|4-2|,它在数轴上的意义是表示数4的点和表示数2的点之间的距离.
类似地,(1)写出式子|a-5|在数轴上的意义是,
(2)写出式子|b+4|在数轴上的意义是,
(3)若|x+2|=3,则x=.
(4)若|x-1|+|x-2|=3,则x为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
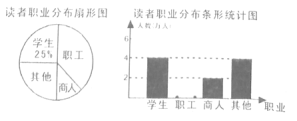
【题目】学习成为现代人的时尚,我,市有关部门统计了最近6个月到图书馆的读者和职业分布情况,并做了下列两个不完整的统计图.请你根据图中提供的信息,解答下列问题:
(l)求在统汁的这段时问内,到图书馆阅读的总人次:
(2)请补全条形统汁图,并求扇形统计图中表示“商人”的扇形的圆心角度数;
(3)符5月份到图书馆的读者共20000人次,估汁其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△![]() 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的宽各为多少米,设与墙平行的一边长为x米. 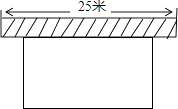
(1)填空:(用含x的代数式表示)另一边长为米;
(2)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=a+(-b)=∣a-b∣;

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 .
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=2,那么x为 ;
(3)当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com