练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，圆O的半径为5，BC⊥OA，OD⊥AB，求OD2+CD2的值．
    考点：垂径定理,直角三角形斜边上的中线,勾股定理
    专题：
    分析：证明AD=BD；进而证明CD是直角△ABC斜边的中线，得到CD=BD；由勾股定理即可解决问题．
    解答：解：∵OD⊥AB，
    ∴AD=BD；
    又∵BC⊥OA，
    ∴CD是直角△ABC斜边的中线，
    ∴CD=BD；由勾股定理得：
    OD2+BD2=OB2，而OB=5，
    ∴OD2+CD2=25．
    点评：该题主要考查了垂径定理、勾股定理等几何知识点的应用问题；牢固掌握定理是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    一架飞机飞行于两城市之间，顺风时要5小时，逆风时要6小时，已知风速每小时24千米．若设两城市之间的距离为x千米，飞机的速度为y千米．则所列方程组为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线AD交⊙O于点B，D，⊙O的半径为10cm，AO=16cm，∠A=30°，OC⊥AD于点C，求BC，AB，AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

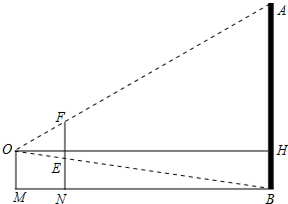    一建筑物AB，眼睛位于点O处，用一把长为22cm的刻度尺EF在眼前适当地运动，使眼睛刚好看不见建筑物AB，这时量得眼睛和刻度尺的距离MN为10cm，眼睛距建筑物的距离MB为20m，问建筑物AB多高？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△AOB中，∠O=90°，AB=5cm，OA=4cm．
    （1）填空：OB=
     
    cm．
    （2）现将△AOB沿射线OB的方向平行移动后得到△DEF．
    ①当移动的距离为多少时，线段AB所扫过的面积是△AOB面积的4倍．
    ②当移动的距离是多少时，∠ABD是直角？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，A，B，C为⊙O上的三点，且有
    AB
    =
    BC
    =
    CA
    ，连接AB，BC，AC．
    （1）试确定三角形ABC的形状并说明理由；
    （2）若⊙O的半径为1，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，EF=2，则BF的长为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，斜边AB=3，若OC∥AB，∠BOC=30°，则下列说法错误的是（　　）
    A、点A到OB的距离为
    1
    2
    B、点A到OC的距离为
    		3
    2
    C、点B到OA的距离为
    		3
    2
    D、点B到OC的距离为
    		3
    4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    （1）4（2x+3）=8（1-x）-5（x-2）
    （2）x-
    2-18x
    3
    =
    x
    9
    +2．

    查看答案和解析>>

    同步练习册答案