
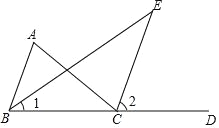
����Ŀ����ͼ����֪�ڡ�ABC�У�CE����ǡ�ACD��ƽ���ߣ�BE�ǡ�ABC��ƽ���ߣ�
(1)��֤����A��2��E��������С����֤�����̣�������������д���ɣ�
֤�����ߡ�ACD�ǡ�ABC��һ����ǣ���2�ǡ�BCE��һ����ǣ�(��֪)
���ACD����ABC+��A����2����1+��E(_________)
���A����ACD����ABC����E����2����1(��ʽ������)
��CE����ǡ�ACD��ƽ���ߣ�BE�ǡ�ABC��ƽ����(��֪)
���ACD��2��2����ABC��2��1(_______)
���A��2��2��2��1(_________)
��2(��2����1)(_________)
��2��E(��������)
(2)�����A����ABC����֤��CE��AB��
���𰸡�(1)��������(2)֤��������.
��������
��1�����ݽ�ƽ���ߵ������Լ���������ǵ����ʼ�����֤��
��2���ɣ�1����֪����A��2��E�����ڡ�A����ABC����ABC��2��ABE�����ԡ�E����ABE���Ӷ���֤AB��CE��
�⣺(1)�ߡ�ACD����ABC��һ����ǣ���2����BCE��һ����ǣ�(��֪)��
���ACD����ABC+��A����2����1+��E(��������ǵ�����)��
���A����ACD����ABC����E����2����1(��ʽ������)��
��CE����ǡ�ACD��ƽ���ߣ�BE�ǡ�ABC��ƽ����(��֪)��
���ACD��2��2����ABC��2��1(��ƽ���ߵ����� )��
���A��2��2��2��1( ��������)��
��2(��2����1)(��ȡ������)��
��2��E(��������)��
(2)��(1)��֪����A��2��E
�ߡ�A����ABC����ABC��2��ABE��
��2��E��2��ABE��
����E����ABE��
��AB��CE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ķ���
�Ķ���![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ����������ϣ���
����������ϣ���![]() Ϊ
Ϊ![]() ���ϵĵ㣬
���ϵĵ㣬 ![]() ������������
������������![]() �ڵ�һ�����ڵ�ͼ����
�ڵ�һ�����ڵ�ͼ����![]() ��
��![]() ���ϵĵ�
���ϵĵ�![]() .
.
(1)��![]() ��
��![]() ��ֵ�ͷ����������ı���ʽ.
��ֵ�ͷ����������ı���ʽ.
(2)������![]() ��һ���۵���ʹ��
��һ���۵���ʹ��![]() ���
���![]() �غϣ��ۺ۷ֱ���
�غϣ��ۺ۷ֱ���![]() �ᣬ
�ᣬ ![]() �������ύ�ڵ�
�������ύ�ڵ�![]() �����߶�
�����߶�![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��ƽ��ֱ������ϵ�е�һ�����ڣ����߶�AOƽ�����߶�BC�����е�A���B��Ӧ��
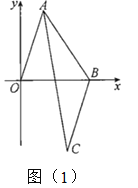
��1����ͼ��1������![]()
![]() ������AB��AC�����������ϴ���һ��D��ʹ��
������AB��AC�����������ϴ���һ��D��ʹ��![]() �����D�����ꣻ
�����D�����ꣻ
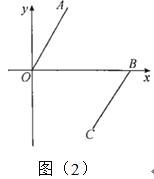
��2����ͼ��2������![]() ����PΪy����һ���㣨��P����ԭ���غϣ�����ֱ��д��
����PΪy����һ���㣨��P����ԭ���غϣ�����ֱ��д��![]() ��
��![]() ֮���������ϵ������֤������
֮���������ϵ������֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η��̣�M��ax2+bx+c=0�� N��cx2+bx+a=0������ac��0��a��c�������ĸ����ۣ�
���������M����������ȵ�ʵ��������ô����NҲ����������ȵ�ʵ������
���������M������������ͬ����ô����N����������Ҳ��ͬ��
�����m�Ƿ���M��һ��������ô![]() �Ƿ���N��һ������
�Ƿ���N��һ������
���������M�ͷ���N��һ����ͬ�ĸ�����ô���������x=1
��ȷ�ĸ����ǣ�������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ļ�����ʽ��
1��2��1��4��2��2��1��2��3��2��1��9��3��3��
1��2��3��4��3��2��1��16��4��4��![]() ��
��
�������漸����Ĺ��ɣ�����������⣺
1��2��3��4��5��6��7��8��9��8��7��6��5��4��3��2��1��ֵΪ__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
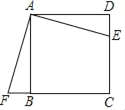
����Ŀ���ı���ABCD�������Σ�E��F�ֱ���DC��CB���ӳ����ϵĵ㣬��DE=BF������AE��AF��EF��
��1����֤����ADE�ա�ABF��
��2����գ���ABF��������ADE����ת������ ���㣬��˳ʱ�뷽����ת�� ���ȵõ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ�������ů���£�Щ�����ڻ�����ʧ���ڱ���|��ʧ12���һ�ֵ͵�ֲ��̦���Ϳ�ʼ����ʯ��������ÿһ��̦���᳤�ɽ��Ƶ�Բ����̦��ֱ���������������Ƶ��������µĹ�ϵʽ��d=7![]() (t��12)������d��ʾ̦��ֱ������λ�����ף�t����������ʧ��ʱ��(��λ����)��
(t��12)������d��ʾ̦��ֱ������λ�����ף�t����������ʧ��ʱ��(��λ����)��
(1)���������ʧ16���̦��ֱ��Ϊ��������?
(2)������һЩ̦��ֱ����35���ף��ʱ���Լ���ڶ�����ǰ��ʧ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��������m�������ݿ��������������ɸ����������ĺͣ���23=3+5��33=7+9+11��43=13+15+17+19������m3���Ѻ�������һ��������2015����m��ֵ�ǣ� ��
A.43B.44C.45D.46
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y =-x+7������������y=![]() x��ͼ���ڵ�A������x�ύ�ڵ�B��
x��ͼ���ڵ�A������x�ύ�ڵ�B��
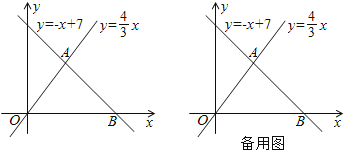
��1�����A�͵�B��������
��2������A��AC��y���ڵ�C������B��ֱ��l��y��������P�ӵ�O��������ÿ��1����λ�����ٶ�����O��C��A��·�����A�˶���ͬʱֱ��l�ӵ�B����������ͬ�ٶ�����ƽ�ƣ���ƽ�ƹ����У�ֱ��l��x���ڵ�R��������BA���߶�AO�ڵ�Q������P�����Aʱ����P��ֱ��l��ֹͣ�˶������˶������У��趯��P�˶���ʱ��Ϊt����
����tΪ��ֵʱ����A��P��RΪ����������ε����Ϊ8��
���Ƿ������A��P��QΪ�������������ֱ���������������ڣ���t��ֵ���������ڣ���˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com