
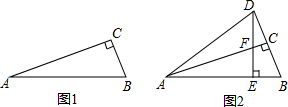
 如图1,在△ABC中,∠C=90°,AB=1,∠A=α,则cosα=$\frac{AC}{AB}$=AC.现在将△ABC沿AC折叠,得到△ADC,如图2,易知B,C,D三点共线,∠DAB=2α(其中0°<α<45°).
如图1,在△ABC中,∠C=90°,AB=1,∠A=α,则cosα=$\frac{AC}{AB}$=AC.现在将△ABC沿AC折叠,得到△ADC,如图2,易知B,C,D三点共线,∠DAB=2α(其中0°<α<45°).分析 (1)先根据勾股定理计算出AC=$\frac{2\sqrt{2}}{3}$,则根据正弦和余弦的定义得到cosα=$\frac{2\sqrt{2}}{3}$,sinα=BC=$\frac{1}{3}$,然后根据题中的结论cos2α=1-2sin2α进行计算;
(2)根据三角函数的定义,在Rt△BDE中得到cos∠BDE=$\frac{DE}{BD}$,则DE=2sinα•cosα,然后在Rt△ADE中得到sin∠DAE=$\frac{DE}{AD}$,即有sin2α=2sinα•cosα.
解答 解:(1)在Rt△ABC中,∵AB=1,BC=$\frac{1}{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\frac{2\sqrt{2}}{3}$,
∴cosα=$\frac{2\sqrt{2}}{3}$,
sinα=BC=$\frac{1}{3}$,
∴cos2α=1-2×($\frac{1}{3}$)2=$\frac{7}{9}$;
故答案为:$\frac{2\sqrt{2}}{3}$,$\frac{7}{9}$;
(2)根据题意得BD=2sinα,∠BDE=α,
在Rt△BDE中,∵cos∠BDE=$\frac{DE}{BD}$,
∴DE=BD•cosα=2sinα•cosα,
在Rt△ADE中,∵sin∠DAE=$\frac{DE}{AD}$
∴sin2α=$\frac{2sinα•cosα}{1}$=2sinα•cosα.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了阅读理解能力.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com