
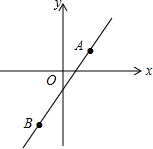
 如图,直线AB经过点A(1,1)和点B(-1,-3).
如图,直线AB经过点A(1,1)和点B(-1,-3).分析 (1)设直线AB的解析式为y=kx+b,将A(1,1)和点B(-1,-3)代入,利用待定系数法即可求出函数解析式;
(2)求出函数与x轴、y轴的交点坐标,后根据三角形的面积公式即可求解.
解答 解:(1)设直线AB的解析式为y=kx+b,
∵直线AB经过点A(1,1)和点B(-1,-3),
∴$\left\{\begin{array}{l}{k+b=1}\\{-k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$.
∴函数的解析式为:y=2x-1;
(2)∵y=2x-1,
∴当x=0,y=-1,当y=0,x=$\frac{1}{2}$,
∴此函数与x轴、y轴围成的三角形的面积为:$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$.
点评 本题考查了待定系数法求一次函数解析式及三角形的面积,难度不大,属于基础题,注意细心运算即可.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
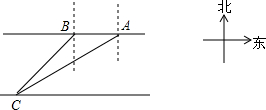 一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)
一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
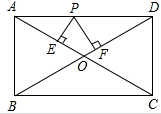 已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm.P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会不会随着点P的一定(不与A、C重合)而改变呢?请说明理由.
已知矩形ABCD中,对角线交于点O,AB=6cm,BC=8cm.P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会不会随着点P的一定(不与A、C重合)而改变呢?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com