
【题目】如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.
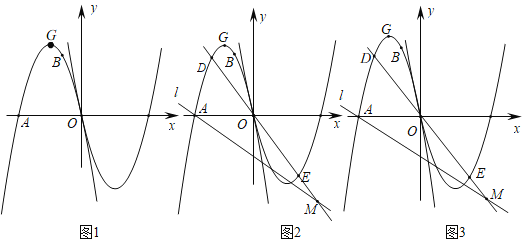
(1)求抛物线C的函数解析式及顶点G的坐标;
(2)如图2,直线l:y=kx![]() 经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;
经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;
(3)如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣4x,顶点为:G(﹣2,4);(2)-3;(3)存在,点P的横坐标为:![]() 或
或![]()
【解析】
(1)运用待定系数法将A(﹣4,0)、B(﹣1,3)代入y=ax2+bx中,即可求得a和b的值和抛物线C解析式,再利用配方法将抛物线C解析式化为顶点式即可求得顶点G的坐标;
(2)根据抛物线C绕点O旋转180°,可求得新抛物线C′的解析式,再将A(﹣4,0)代入y=kx![]() 中,即可求得直线l解析式,根据对称性可得点E坐标,过点D作DF⊥x轴于F,过M作MR⊥x轴于R,由DE=2EM,建立方程求解即可;
中,即可求得直线l解析式,根据对称性可得点E坐标,过点D作DF⊥x轴于F,过M作MR⊥x轴于R,由DE=2EM,建立方程求解即可;
(3)连接BG,易证△ABG是Rt△,∠ABG=90°,可得tan∠DEP=tan∠GAB![]() ,在x轴下方过点O作OH⊥OE,在OH上截取OH
,在x轴下方过点O作OH⊥OE,在OH上截取OH![]() OE
OE![]() ,过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;通过建立方程组求解即可.
,过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;通过建立方程组求解即可.
(1)将A(﹣4,0)、B(﹣1,3)代入y=ax2+bx中,得![]() ,
,
解得![]() ,
,
∴抛物线C解析式为:y=﹣x2﹣4x,
配方,得:y=﹣x2﹣4x=﹣(x+2)2+4,
∴顶点为:G(﹣2,4);
(2)∵抛物线C绕点O旋转180°,得到新的抛物线C′.
∴新抛物线C′的顶点为:G′(2,﹣4),二次项系数为:a′=1,
∴新抛物线C′的解析式为:y=(x﹣2)2﹣4=x2﹣4x,
将A(﹣4,0)代入y=kx![]() 中,得0=﹣4k
中,得0=﹣4k![]() ,解得k
,解得k![]() ,
,
∴直线l解析式为y![]() x
x![]() ,
,
设D(m,﹣m2﹣4m),
∵D、E关于原点O对称,
∴OD=OE,
∵DE=2EM,
∴OM=2OD,
过点D作DF⊥x轴于F,过M作MR⊥x轴于R,
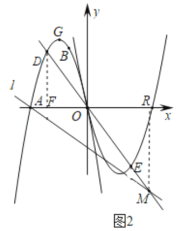
∴∠OFD=∠ORM,
∵∠DOF=∠MOR,
∴△ODF∽△OMR,
∴![]() 2,
2,
∴OR=2OF,RM=2DF,
∴M(﹣2m,2m2+8m) ,
将M(﹣2m,2m2+8m)代入直线l解析式y![]() x
x![]() ,
,
∴2m2+8m![]() (﹣2m)
(﹣2m)![]() ,
,
解得:m1=﹣3,m2![]() ,
,
∵m<﹣2
∴m的值为:﹣3;
(3)由(2)知:m=﹣3,
∴D(﹣3,3),E(3,﹣3),OE=3![]() ,
,
如图3,连接BG,

在△ABG中,
∵AB2=(﹣1+4)2+(3﹣0)2=18,
BG2=(﹣1+2)2+(3﹣4)2=2,
AG2=(﹣4+2)2+(0﹣4)2=20,
∴AB2+BG2=AG2,
∴△ABG是直角三角形,∠ABG=90°,
∴tan∠GAB![]() ,
,
∵∠DEP=∠GAB,
∴tan∠DEP=tan∠GAB![]() ,
,
在x轴下方过点O作OH⊥OE,在OH上截取OH![]() OE
OE![]() ,
,
过点E作ET⊥y轴于T,连接EH交抛物线C于点P,点P即为所求的点;
∵E(span>3,﹣3),
∴∠EOT=45°,
∵∠EOH=90°,
∴∠HOT=45°,
过点H作HN⊥y轴于N,
∵OH![]() ,∠HOT=45°,
,∠HOT=45°,
∴HN=NO=1,
∴H(﹣1,﹣1),设直线EH解析式为y=px+q,
则![]() ,解得
,解得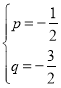 ,
,
∴直线EH解析式为y![]() x
x![]() ,
,
解方程组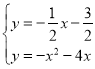 ,
,
得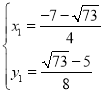 ,
,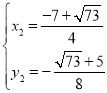 ,
,
∴点P的横坐标为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
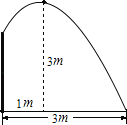
【题目】要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷头,使喷出的抛物线形水柱在与水池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离中心3m.
(1)在给定的坐标系中画出示意图;
(2)求出水管的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
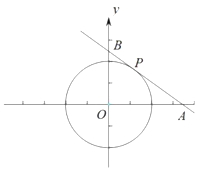
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画![]() ,P是
,P是![]() 上一动点,且P在第一象限内,过点P作
上一动点,且P在第一象限内,过点P作![]() 的切线与x轴相交于点A,与y轴相交于点B.在
的切线与x轴相交于点A,与y轴相交于点B.在![]() 上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
上存在点Q,使得以Q、O、A、P为顶点的四边形是平行四边形,请写出Q点的坐标_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于点E.
(1)如图①,若CD=8,BE=2,求⊙O的半径;
(2)如图②,点G是![]() 上一点,AG的延长线与DC的延长线交于点F,求证:∠AGD=∠FGC.
上一点,AG的延长线与DC的延长线交于点F,求证:∠AGD=∠FGC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学考试中,小明有一道选择题(只能在四个选项A、B、C、D中选一个)不会做,便随机选了一个答案;小亮有两道选择题都不会做,他也随机选了两个答案.
(1)小明随机选的这个答案,答对的概率是 ;
(2)通过画树状图或列表法求小亮两题都答对概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
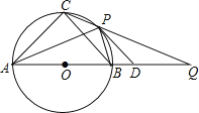
【题目】如图,⊙O为等腰三角形ABC的外接圆,AB是⊙O的直径,AB=12,P为![]() 上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则
上任意一点(不与点B,C重合),直线CP交AB的延长线于点Q,⊙O在点P处的切线PD交BQ于点D,则下列结论:①若∠PAB=30°,则![]() 的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6
的长为π;②若PD∥BC,则AP平分∠CAB;③若PB=BD,则PD=6![]() ;④无论点P在
;④无论点P在![]() 上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
上的位置如何变化,CPCQ=108.其中正确结论的序号为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
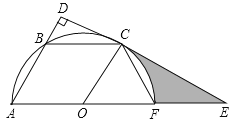
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考察某校300名初中毕业生的身高状况,从中抽出了10名学生,测得身高分别为(单位:cm):165,170,160,150,180,170,165,165,155,150;在这个问题的下列叙述中,错误的是( )
A.300名学生的身高是总体
B.这300名学生的平均身高估计是163(cm)
C.这10名学生身高的众数和中位数是165(cm)
D.这10名学生的身高是样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初三学生每学期参加综合实践活动的情况,随机抽样调查了某校初三学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:

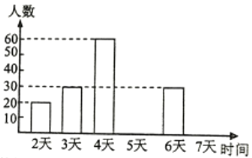
(1)该校初三学生总数为 人;
(2)分别求出活动时间为5天、7天的学生人数为 、 ,并补全频数分布直方图;
(3)扇形统计图中“活动时间为5天”的扇形所对圆心角的度数是 ;
(4)在这次抽样调查中,众数和中位数分别是 、 ;
(5)如果该市共有初三学生96000人,请你估计“活动时间不少于5天”的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com