
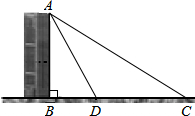
 如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.
如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高. 分析 在Rt△ABC中,设AB=x,则AC=2x,BC=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,在Rt△ABD中,$\frac{x}{\sqrt{3}x-20}$=tan60°,据此即可求出AB的长.
解答 解:在Rt△ABC中,设AB=x,则AC=2x,BC=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
则BD=($\sqrt{3}$x-20)米,
在Rt△ABD中,$\frac{x}{\sqrt{3}x-20}$=tan60°,
$\frac{x}{\sqrt{3}x-20}$=$\sqrt{3}$,
∴x=10$\sqrt{3}$.
答:楼AB的高为10$\sqrt{3}$米.
点评 本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:选择题
| A. | BC=B′C′ | B. | ∠A=∠A′ | C. | ∠C=∠C′ | D. | AC=A′C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.16×103 | B. | 21.6×103 | C. | 0.216×104 | D. | 2.16×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
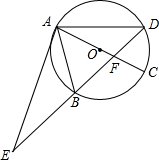 如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.
如图,⊙O的直径AC与弦BD交于点F,点E是DB延长线上的一点,∠EAB=∠ADB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com