
����Ŀ��A.B����֮����һ����ֱ�Ĺ�·���׳���A�س���������B����ʻ����;������ͣ����1Сʱ��ԭ��ʻ��B�أ��ڼ׳�������ͬʱ�ҳ���B�س���������A����ʻ������A�غ�������ԭ·ԭ�ٷ��ص�B�ء���������ʻ�Ĺ����У�����������A�ص�·��y(ǧ��)����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ��ͼ��ʾ������ͼ��ش��������⣺
��1����ͼ�����_____����������ȷ����ֵ
��2����׳�����;����ͣ����ʻ��B�ع����У�y��x֮��ĺ�����ϵʽ
��3��ֱ��д�����ҳ���A�س�������Сʱ��.�������ֱ׳���;ͣ���صľ�����ȣ�

���𰸡���1��6��7 ����2��y=40x-40(3��x��7) ��3�� ![]() Сʱ��
Сʱ��
����������������1�����ݺ���ͼ��ó�AB���صľ��룬���г������������ϵ��·����ʱ��=�ٶȾͿ���������ۣ�
��2�������г������������ϵ���E�����꣬��y��x֮��ĺ�����ϵʽΪ![]() ���ɴ���ϵ�����Ϳ���������ۣ�
���ɴ���ϵ�����Ϳ���������ۣ�
��3�������г������������ϵ����ҳ�������ʱ�䣬��ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ
y��![]() �ɴ���ϵ����������ۣ��루2������ʽ���ɷ����������⼴�ɣ�
�ɴ���ϵ����������ۣ��루2������ʽ���ɷ����������⼴�ɣ�
��⣺(1)�ɺ���ͼ��
A.B���صľ���Ϊ��240ǧ��,
�׳����ٶ�Ϊ��80��2=40ǧ��/Сʱ��
�ҳ����ٶ�Ϊ��240��3=80ǧ��/Сʱ.
![]()
![]()
![]()
�ʴ�Ϊ��6��7.
(2)�����⣬��
D(3,80).![]()
��y��x֮��ĺ�����ϵʽΪy=kx+b�������⣬��
![]() ��ã�
��ã�![]()
��y=40x40.
��y��x֮��ĺ�����ϵʽΪy=40x40![]() ��
��
(3)�����⣬��
![]()
��ֱ��FG�Ľ���ʽΪy��![]() ������,��
������,��
![]() ��ã�
��ã�![]()
��y��![]()
![]()
��ã�![]()
![]()
���ҳ���A�س���![]() Сʱʱ,��׳���;ͣ���صľ������.
Сʱʱ,��׳���;ͣ���صľ������.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж�����ı�����ƽ���ı��ε���

A��AB��DC��AD��BC����B��AB=DC��AD=BC
C��AO=CO��BO=DO�� ��D��AB��DC��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���A����B����C�ĶԱ߷ֱ�Ϊa��b��c������˵���д�������� ��
A�������C����B����A������ABC��ֱ�������Σ�����C��90��
B�����![]() ������ABC��ֱ�������Σ�����C��90��
������ABC��ֱ�������Σ�����C��90��
C�������c��a���� c��a����![]() ������ABC��ֱ�������Σ�����C��90��
������ABC��ֱ�������Σ�����C��90��
D�������A����B����C��3��2��5������ABC��ֱ�������Σ�����C��90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB=20��BC=6����Ϊ���±ߵ��е㣬PΪCD���ϵĵ㣬����AEP������Ϊ10�ĵ��������Σ����߶Σ£еij�Ϊ______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧҪ����ij�̴ѵĸ߶ȣ�����һ�澵�ӷ��������̴�֮��ĵ�����ijһλ�ã�Ȼ��վ���뾵�ӡ��̴ѳ�һ��ֱ�ߵĵط����պôӾ��п����̴ѵĶ������������ͬѧ����Ϊ1.65�ף��������ӵľ�����2�ף���þ��浽�̴ѵľ���Ϊ20�ף��̴ѵĸ߶�_____ ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽�����ⱳ����ѧ����ϣ���ʦ��һ�����dz߰�ͼ��1����ʾλ�ðڷţ��ֱ�������AOC����BOD��ƽ����OM��ON��Ȼ������������⣺�����MON�Ķ�����
����̽������ȤС�顱��ͬѧ��������������̽����ʦ��������⣬���ǽ����dz߷ֱ�ͼ2��ͼ3��ʾ�ķ�ʽ�ڷţ�OM��ON��Ȼ�ǡ�AOC�͡�BOD�Ľ�ƽ���ߣ����У���ͼ2��ʽ�ڷ�ʱ�����Կ�����ON��OD��OB��ͬһֱ���ϣ���ͼ3��ʽ�ڷ�ʱ����AOC�͡�BOD��ȣ�
��1�������������ȤС�顱���м��㣺ͼ2�С�MON�Ķ���Ϊ�� ���㣮ͼ3�С�MON�Ķ���Ϊ�� ���㣮
���ָ���
�����ͼ2��ͼ3��ʾ�������ȤС�顱�ֶ�ͼ1��ʾ������������ۣ�
С��������ͼ1�С�AOC�͡�BOD�ĺ�Ϊ90�㣬�����������õ���MOC�͡�NOD�ĺͣ��������������MON�Ķ�����
С�������BODΪx�㣬���Ǿ����ú�x��ʽ�ӷֱ��ʾ����NOD�͡�MOC����������Ҳ�������MON�Ķ�����
��2������������ǵ�̸�����ݣ����ͼ1�С�MON�Ķ�����
�����չ
�ܵ�����ȤС�顱�����������ǻ�С�顱�����dz߰�ͼ4��ʾ��ʽ�ڷţ��ֱ�������AOC����BOD��ƽ����OM��ON��������ΪҲ�������MON�Ķ�����
��3����ͬ�⡰�ǻ�С�顱�Ŀ�������ͬ�⣬�����MON�Ķ���������ͬ�⣬��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ��������O������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB������һ��ON��ֱ��AB���·���

��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM����BOC���ڲ�����ǡ��ƽ����BOC��������ʱֱ��ON�Ƿ�ƽ����AOC����˵��������
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ���˳ʱ�뷽����תһ��������ת�Ĺ���������t��ʱ��ֱ��ONǡ��ƽ�������AOC���� t��ֵΪ �루ֱ��д���������
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON����AOC���ڲ�����̽��������ת����������AOM����NOC�IJ��Ƿ����仯��������������������ֵ�����仯���������ı仯��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩С��ϲ���о���ѧ���⣬�ڼ�����ʽ�Ӽ�����4x2��7+5x��+��2x+3x2����ʱ���뵽��Сѧ������ʽ�Ӽ�������A����4x2��7+5x��B��2x+3x2��Ȼ��������ʽ����x���н������У�A����4x2+5x��7��B��3x2+2x�����ֻҪд�������ϵ������ͬ���������ʽ�������£�
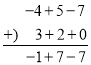
���ԣ�����4x2��7+5x��+��2x+3x2������x2+7x��7��
��ģ�½��⣩��A����4x2y2+2x3y��5xy3+2x4��B��3x3y+2x2y2��y4��4xy3�����㰴��С���ķ������ȶ���ʽA��B����ij����ĸ���н������У���д�������ϵ��������ʽ����A��B����д��A��B��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������ͼ�٣�AB��CD��EF����G��P��H�ֱ���ֱ��AB��CD��EF�ϣ�����PG��PH������P��ֱ��GH�����ʱ����˵����AGP+��EHP����GPH����������������Ľ�����̣����������Ľ�����̣�����գ����ɻ���ѧʽ����

�⣺��ͼ�٣���AB��CD���� ����
���AGP����GPD
��CD��EF
���DPH����EHP���� ����
�ߡ�GPD+��DPH����GPH��
���AGP+��EHP����GPH���� ����
��չ����ͼ�ٵĵ�P�ƶ���ֱ��GH���Ҳ࣬�����������䣬��ͼ�ڣ���̽����AGP����EHP����GPH֮��Ĺ�ϵ����˵�����ɣ�
Ӧ�ã���ͼ�ۣ�AB��CD��EF����G��H�ֱ���ֱ��AB��EF�ϣ���Q��ֱ��CD�ϵ�һ�����㣬�Ҳ���ֱ��GH�ϣ�����QG��QH������GQH��70�������AGQ+��EHQ���� ���ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com